
分析 (1)利用已知条件通过Sn+1-Sn=an+1,推出{an}为公差等于2的等差数列,然后求解通项公式.
(2)化简bn=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$$({\frac{1}{2n-1}-\frac{1}{2n+1}})$,利用裂项消项法求解数列的和,通过数列的单调性推出结果即可.
解答 解:(1)因为(an+1)2=4Sn,所以Sn=$\frac{({a}_{n}+1)^{2}}{4}$,Sn+1=$\frac{({a}_{n+1}+1)^{2}}{4}$.
所以Sn+1-Sn=an+1=$\frac{({a}_{n+1}+1)^{2}-({a}_{n}+1)^{2}}{4}$,
即4an+1=an+12-an2+2an+1-2an,∴2(an+1+an)=(an+1+an)(an+1-an)…(4分)
因为an+1+an≠0,所以an+1-an=2,
即{an}为公差等于2的等差数列.由(a1+1)2=4a1,解得a1=1,所以an=2n-1…(6分)
(2)由(1)知bn=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$$({\frac{1}{2n-1}-\frac{1}{2n+1}})$,
∴Tn=b1+b2+…+bn=$\frac{1}{2}$$({1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1}})=\frac{1}{2}({1-\frac{1}{2n+1}})$
=$\frac{1}{2}$-$\frac{1}{2(2n+1)}$…(8分)
∵Tn+1-Tn=$\frac{1}{2}$-$\frac{1}{2(2n+3)}$-$({\frac{1}{2}-\frac{1}{2(2n+1)}})$=$\frac{1}{2(2n+1)}$-$\frac{1}{2(2n+3)}$
=$\frac{1}{(2n+1)(2n+3)}$>0,
∴Tn+1>Tn.∴数列{Tn}为递增数列,…(10分)
∴Tn的最小值为T1=$\frac{1}{2}$-$\frac{1}{6}$=$\frac{1}{3}$.所以$\frac{1}{3}≤{T_n}<\frac{1}{2}$…(12分)
点评 本题考查数列的递推关系式的应用,数列的判断,数列求和的方法,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
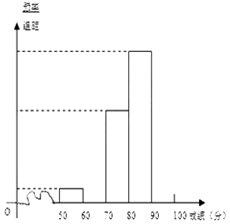 中日“钓鱼岛争端”问题越来越引起社会关注,我校对高二600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高二600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.| 分 组 | 频 数 | 频 率 |
| [50,60) | 2 | 0.04 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.2 |
| [80,90) | 16 | 0.32 |
| [90,100] | 14 | 0.28 |
| 合 计 | 50 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
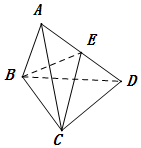 如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
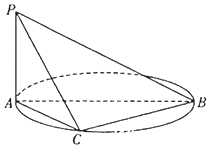 如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com