
����Ŀ��ij������������ ��������APP����չ�������ֽ��������Աÿ����5ǧ���ɻ����30�֣�����5ǧ�������֣���ÿ����2ǧ���ٻ�20�֣�����2ǧ�������֣���Ϊ�˽��Ա�Ľ����������������ij���ϵͳ�������ȡ��1000����Ա��ͳ���˵������ǵIJ����������������ݷ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ���飬�����õ�����Ƶ�ʷֲ�ֱ��ͼ��
���飬�����õ�����Ƶ�ʷֲ�ֱ��ͼ��
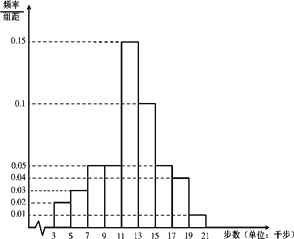
������������1000����Ա�в�������11ǧ����������
�������ӵ��첽����![]() ��
�� ![]() ��
�� ![]() �Ļ�Ա�а��ֲ�����ķ�ʽ��ȡ6�ˣ��ٴ���6���������ȡ2�ˣ�����2�˻���֮�Ͳ�����200�ֵĸ��ʣ�
�Ļ�Ա�а��ֲ�����ķ�ʽ��ȡ6�ˣ��ٴ���6���������ȡ2�ˣ�����2�˻���֮�Ͳ�����200�ֵĸ��ʣ�
������д���������ݵ���λ����ֻд�������
���𰸡�(1) 300��;(2) ![]() ;(3)
;(3) ![]() .
.
�������������������1���������ηֲ�ֱ��ͼ�е����ݵõ������ߵIJ�����![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ��
��
��![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ����
����![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() �����õ�300�ˣ���2�����ݷֲ�����ĸ���õ���
�����õ�300�ˣ���2�����ݷֲ�����ĸ���õ���![]() ��Ӧ��ȡ3�ˣ�ÿ�˵Ļ�����90�֣���
��Ӧ��ȡ3�ˣ�ÿ�˵Ļ�����90�֣���![]() ��Ӧ��ȡ2�ˣ�ÿ�˵Ļ�����110�֣���
��Ӧ��ȡ2�ˣ�ÿ�˵Ļ�����110�֣���![]() ��Ӧ��ȡ1�ˣ�ÿ�˵Ļ�����130�֣��ٸ��ݹŵ���͵Ĺ�ʽ�õ�����ֵ����3������λ���ĸ������ֱ��ͼ��������.
��Ӧ��ȡ1�ˣ�ÿ�˵Ļ�����130�֣��ٸ��ݹŵ���͵Ĺ�ʽ�õ�����ֵ����3������λ���ĸ������ֱ��ͼ��������.
������
��������1000����Ա�н����ߵIJ�����![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ��
��
�����ߵIJ�����![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ��
��
�����ߵIJ�����![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ��
��
�����ߵIJ�����![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ��
��
![]() ��
��
������1000����Ա�н����ߵIJ�������11ǧ��������Ϊ300����
���������ֲ�����ķ�������![]() ��Ӧ��ȡ3������Ϊ
��Ӧ��ȡ3������Ϊ![]() ��
�� ![]() ��
�� ![]() ��ÿ�˵Ļ�����90����
��ÿ�˵Ļ�����90����
��![]() ��Ӧ��ȡ2�ˣ���Ϊ
��Ӧ��ȡ2�ˣ���Ϊ![]() ��
�� ![]() ��ÿ�˵Ļ�����110����
��ÿ�˵Ļ�����110����
��![]() ��Ӧ��ȡ1�ˣ���Ϊ
��Ӧ��ȡ1�ˣ���Ϊ![]() ��ÿ�˵Ļ�����130����
��ÿ�˵Ļ�����130����
��6���������ȡ2������![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��15�ַ�����
��15�ַ�����
���Դ�6���������ȡ2�ˣ���2�˵Ļ���֮�Ͳ�����200�ֵ���![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��12�ַ�����
��12�ַ�����
���6���������ȡ2�ˣ���2�˵Ļ���֮�Ͳ�����200��Ϊ�¼�![]() ����
����
![]() ��
��
���Դ�6���������ȡ2�ˣ���2�˵Ļ���֮�Ͳ�����200�ֵĸ���Ϊ![]() ��
��
��������λ��Ϊ![]() ��
��


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ʱ��������
ʱ��������![]() �ĵ�����
�ĵ�����![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
�� ![]() ���㣬�������ֱ�Ϊ
���㣬�������ֱ�Ϊ![]() ��
�� ![]() ���߶�
���߶�![]() ���е�ĺ�����Ϊ
���е�ĺ�����Ϊ![]() ����
����![]() ��
�� ![]() ǡΪ����
ǡΪ����![]() ����㣬��֤��
����㣬��֤�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����SnΪ����{an}��ǰn��ͣ���֪![]() ��
��
������{an}��ͨ�ʽ��
������![]() ��������{bn}��ǰn���Tn��
��������{bn}��ǰn���Tn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
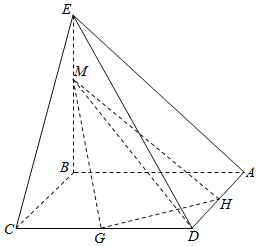
����Ŀ����ͼ��ʾ��EB��ֱ������ABCD����ƽ�棬��EB=BC=2����BAD=60������G��H�ֱ�Ϊ��CD��DA���е㣬��M���߶�BE�ϵĶ��㣮
��I����֤��GH��DM��
��II��������D-MGH��������ʱ�����A����MGH�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ź�����Ѿ���Ϊ�й����ջ��ȴ���ʱ�dz�ϲ����һ����С���ռ�����20��ͬѧ���괺���ڼ�����������![]() ��Ԫ�����£���������ȡ��������
��Ԫ�����£���������ȡ��������
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
����20�����ݽ��з��飬�����Ƶ�����£�
��� | ��������� | Ƶ�� |
|
| 2 |
|
| 9 |
|
|
|
|
| 3 |
|
|
|
������д����ֵ�����ش���20��ͬѧ�����ĺ��������λ�������ĸ����
��������![]() ��������ƽ�����뷽��ֱ�Ϊ
��������ƽ�����뷽��ֱ�Ϊ![]() ��������ƽ�����뷽��ֱ�Ϊ
��������ƽ�����뷽��ֱ�Ϊ![]() ���Էֱ�Ƚ�
���Էֱ�Ƚ�![]() ��
��![]() ��
��![]() ��
��![]() �Ĵ�С����ֻ��д�����ۣ�
�Ĵ�С����ֻ��д�����ۣ�
��������![]() �����������������ȡ2�����ݣ�����2�����ݲ�ľ���ֵΪ
�����������������ȡ2�����ݣ�����2�����ݲ�ľ���ֵΪ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λѧ���μ���ѧ������ѵ���ֱַ����������ѵ�ڼ�μӵ����ɴ�Ԥ���ɼ��������ȡ8�Σ���¼���£�
�ף�82��81��79��78��95��88��93��84���ң�92��95��80��75��83��80��90��85
��1�� �þ�Ҷͼ��ʾ���������ݣ�������ƽ�����뷽�
��2����Ҫ����ѡ��һ�˲μ���ѧ��������ͳ��ѧ�ĽǶȣ���ƽ�������������������������ǣ�����Ϊѡ����λѧ���μӺ��ʣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�
��1����֤��cos2![]() +cos2
+cos2![]() =1��
=1��
��2����cos��![]() +A��sin��
+A��sin��![]() ��+B��tan��C���У���0����֤����ABCΪ�۽������Σ�
��+B��tan��C���У���0����֤����ABCΪ�۽������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ���Һ���
���Һ���![]() ��ż����.
��ż����.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������ʽ![]() ��
��![]() �Ϻ��������
�Ϻ��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������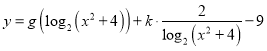 ǡ����������㣬��
ǡ����������㣬��![]() ��ֵ���ú��������.
��ֵ���ú��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽��У��ý���ѧ�ռ�������������䰴�ֲ�����ķ�ʽ�����˸�У50����ʦ�����ǵ�����Ƶ����ʹ�ö�ý���ѧ����������ֲ����±���

��1��������ͳ��������������![]() �����������ж��Ƿ���
�����������ж��Ƿ���![]() �İ�����Ϊ��40��Ϊ�ֽ����Ƿ�ʹ�ö�ý���ѧ�в��죿
�İ�����Ϊ��40��Ϊ�ֽ����Ƿ�ʹ�ö�ý���ѧ�в��죿

����![]() ��
��![]() .
.

��2�������÷ֲ�����ķ�ʽ���������40���Ҿ���ʹ�ö�ý��Ľ�ʦ��ѡ��6�ˣ��ٴ���6���������ȡ2�ˣ�����2����������1��������30-39��ĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com