
����Ŀ����֪��������{an}��ǰn���ΪSn��������a1��2��anan+1��2(Sn��1) (![]() )��
)��
��1��������{an}��ͨ�ʽ��
��2��������{bn}����b1��1��![]() (
(![]() ��
��![]() )����{bn}��ǰn���Tn��
)����{bn}��ǰn���Tn��
��3��������{cn}����![]() ��
��![]() (
(![]() ��
��![]() )�������Ƿ����������p��q������1 < p < q����ʹc1��cp��cq�ɵȱ����У������ڣ����������������������(p��q)���������ڣ�˵�����ɣ�
)�������Ƿ����������p��q������1 < p < q����ʹc1��cp��cq�ɵȱ����У������ڣ����������������������(p��q)���������ڣ�˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ����3��������.
����3��������.
�������������������1����anan+1��2(Sn��1)���ɵ�an+1an+2��2(Sn+1��1)����ʽ����ɵ�an+2an��2��������ż�ɵ�![]() ����2����
����2����![]() �����������������ɵý������3�������������������(p��q)��ʹc1��cp��cq�ɵȱ����У�
�����������������ɵý������3�������������������(p��q)��ʹc1��cp��cq�ɵȱ����У�![]() �ɵ�
�ɵ�![]() �����⣬��֤��p
�����⣬��֤��p![]() 3ʱ�������⼴��.
3ʱ�������⼴��.
�����������1��������anan+1��2(Sn��1)�� ��
an+1an+2��2(Sn+1��1)�� ��
�ɢ��ڵõ���an+1(an+2an)��2an+1�� ��
��Ϊan+1>0����an+2an��2�� ��
��a1��2���ɢܿ�֪![]() ��a2��3���ɢܿ�֪
��a2��3���ɢܿ�֪![]() ��
��
��ˣ�![]() ��
��
��2����n=1ʱ
��![]() ʱ��
ʱ��![]()
��![]() ��
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��3�������������������(p��q)��ʹc1��cp��cq�ɵȱ����У���c1cq��cp2��
��lgc1��lgcq��2 lgc p�ɵȲ����У����ǣ�![]() (��)��
(��)��
��ʱ��
![]()
![]() ����ʱ��
����ʱ��![]() ��
��
��֪(p��q)=(2��3) ǡΪ����(��)��һ��⣮
�ֵ�p![]() 3ʱ��
3ʱ��![]() <0��������{
<0��������{![]() }(p��3)Ϊ�ݼ����У�
}(p��3)Ϊ�ݼ����У�
����![]() =
=![]() ��
��![]() <0�����Դ�ʱ����(��)���������⣮
<0�����Դ�ʱ����(��)���������⣮
���ϣ�����Ωһ����������(p��q)=(2��3)��ʹc1��cp��cq�ɵȱ����У�
���������硿���������������Ѱ��յ���ͷ���֮һ����ԭ������ʱ�����ҵ�����ķ���ͻ����һ�ѵ�ķ����Ǹ���ʽ�ӵĽṹ�ص㣬����һЩ����������ɣ���![]() ����
����![]()
![]() ����
����![]() ��
��
��![]()
![]() �����⣬��ע������֮�������Ĺ��������׳��ֶ�����������⣬���¼���������.
�����⣬��ע������֮�������Ĺ��������׳��ֶ�����������⣬���¼���������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ���뺯��
���뺯��![]() �й������ߣ�
�й������ߣ�
������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����������ʽ![]() ����
����![]() ��һ��ֵ���������
��һ��ֵ���������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵õ�����y=sin2x��ͼ��ֻ��Ѻ���y=sin��2x�� ![]() ����ͼ�� ��
����ͼ�� ��
A.����ƽ�� ![]() ����λ����
�������
B.����ƽ�� ![]() ����λ����
�������
C.����ƽ�� ![]() ����λ����
�������
D.����ƽ�� ![]() ����λ����
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�������������ȱˮ�Ĺ��ң�ij������Ϊ�˹��������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����![]() ���֣���һλ���������ˮ��������
���֣���һλ���������ˮ��������![]() �IJ��ְ�ƽ���շѣ�����
�IJ��ְ�ƽ���շѣ�����![]() �IJ��ְ�����շ�.Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���
�IJ��ְ�����շ�.Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() �ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
�ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
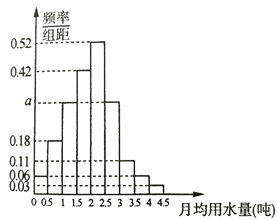
������ֱ��ͼ��![]() ��ֵ��
��ֵ��
��������Ƶ����Ϊ���ʣ��Ӹó��о����������ȡ3�ˣ�����3�����¾���ˮ��������3�ֵ�����Ϊ![]() ����
����![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.
��������������ϣ��ʹ85%�ľ���ÿ�µ���ˮ����������![]() ���֣�������
���֣�������![]() ��ֵ����ȷ��0.01������˵������.
��ֵ����ȷ��0.01������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������4������3�������3�������ҹ�����5������3�������2�������ȴӼ������ȡ��һ������ҹޣ��ֱ���A1��A2��A3��ʾ�ɼ�ȡ�������Ǻ�����ͺ�����¼����ٴ��ҹ������ȡ��һ����B��ʾ���ҹ�ȡ�������Ǻ�����¼������еĽ��ۣ�
��P��B��= ![]() ��
��
��P��B|A1��= ![]() ��
��
���¼�B���¼�A1���������
��A1 �� A2 �� A3������������¼���
��P��B����ֵ����ȷ������Ϊ����A1 �� A2 �� A3����һ�������йأ�
������ȷ���۵����Ϊ �� ������ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ũׯ��һ�鳤��������ABCD��AB=50�ף�BC=25 ![]() �ף�Ϊ�˱����ο�����ɢ������ũׯ�����������ڽ�������ͼ��ʾ�Ĺ۹�����OE��EF��OF�����ǵ�����滮��Ҫ��O��AB���е㣬��E�ڱ�BC�ϣ���F�ڱ�AD�ϣ��ҡ�EOF=90�㣮
�ף�Ϊ�˱����ο�����ɢ������ũׯ�����������ڽ�������ͼ��ʾ�Ĺ۹�����OE��EF��OF�����ǵ�����滮��Ҫ��O��AB���е㣬��E�ڱ�BC�ϣ���F�ڱ�AD�ϣ��ҡ�EOF=90�㣮 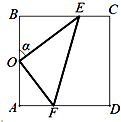
��1�����BOE=�����Խ���OEF���ܳ�l��ʾ�ɦ��ĺ�����ϵʽ��������˺����Ķ�����
��2�������㣬��������ÿ������þ�Ϊ4000Ԫ�����������Ʋ���ʹ�����ܷ�����Ͳ��������ܷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD����B��C����ADΪֱ����Բ�ϣ�AD=2�ף�
(1)��ͼ1��������˿��AB��BC��CD����������ɣ���AB��CD��ÿ�ɷ���1��λ��������BC��ÿ�ɷ���2��λ�����������BC�ij��ȣ�ʹ�õ���˿���������������������������ֵ��
(2)��ͼ2��������˿�ɻ�![]() ����BC����������ɣ��ڻ�
����BC����������ɣ��ڻ�![]() ��ÿ�ɷ���1��λ����������BC��ÿ�ɷ���2��λ�����������BC�ij��ȣ�ʹ�õ���˿��������������
��ÿ�ɷ���1��λ����������BC��ÿ�ɷ���2��λ�����������BC�ij��ȣ�ʹ�õ���˿��������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼���ѧϰ�����ij��ѵ�����ڽ��ھٰ�һ����������ֱ�Ӽס����������ȡ10��ѧԱ�ijɼ�����ͳ�Ʒ�������ɼ��ľ�Ҷͼ��ͼ��ʾ����λ���֣�������ɼ�������90��������Ϊ������ѧԱ��.
��1���ֱ���ס�������ѧԱ�ɼ���ƽ���֣��������һλС������
��2���Ӽװ�4������ѧԱ�г�ȡ���ˣ����Ұ�2��80�����µ�ѧԱ�г�ȡһ�ˣ�������ƽ���ֲ�����90�ֵĸ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ԲC�� ![]() +
+ ![]() =1��a��b��0������ԲC1��x2+y2=a2+b2Ϊ��ԲC�ġ�����Բ������֪��ԲC��������Ϊ
=1��a��b��0������ԲC1��x2+y2=a2+b2Ϊ��ԲC�ġ�����Բ������֪��ԲC��������Ϊ ![]() ���Ҿ����㣨0��1����
���Ҿ����㣨0��1����
��1����ʵ��a��b��ֵ��
��2��������P��0��m����m��0����ֱ��l����ԲC����ֻ��һ�������㣬��l����ԲC�İ���ԲC1���صõ��ҳ�Ϊ2 ![]() ����ʵ��m��ֵ��
����ʵ��m��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com