Question

已知等差数列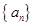的前n项和为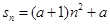，某三角形三边之比为,则该三角形的最大角为       

 

Answer 1

【答案】

【解析】解：令n=1，得到a1=S1=2a+1，令n=2，得到a1+a2=S2=5a+4，

所以a2=3a+3，故公差d=（3a+3）-（2a+1）=a+2，

所以Sn=n（2a+1）+n(n-1) /2 （a+2）=a+2 /2 n²+（2a+1-a+2/ 2 ）n=（a+1）n²+a，

得到a=0，所以等差数列的首项a₁=1，公差d=2，

所以三角形三边之比为3：5：7，设最大的角为α，三边分别为3k，5k，7k，

所以cosα=3k²+5k²-7k²/ 2×3k×5k =-1 2 ，又α∈（0，180°），

则该三角形最大角α为120°．

故答案为：120°