
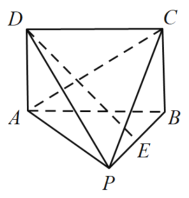
【题目】在四棱锥![]() 中,
中,![]() 为等边三角形,四边形
为等边三角形,四边形![]() 为矩形,
为矩形,![]() 为
为![]() 的中点,
的中点,![]() .
.
![]() 证明:平面
证明:平面![]() 平面
平面![]() .
.
![]() 设二面角
设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的取值范围.
的取值范围.
 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为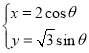 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求曲线![]() 上的动点到直线
上的动点到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(3)当![]() 时,若方程
时,若方程![]() 在区间
在区间![]() 上有唯一解,求
上有唯一解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,有下列四个命题:
,有下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 在
在![]() 是单调函数;
是单调函数;
③当![]() 时,函数
时,函数![]() 恒成立;
恒成立;
④当![]() 时,函数
时,函数![]() 有一个零点,
有一个零点,
其中正确的是____________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com