
【题目】在四棱锥![]() 中,底面
中,底面![]() 是一直角梯形,
是一直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 底面
底面![]() .
.
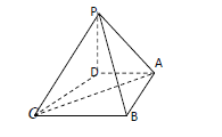
(1)在线段![]() 上是否存在一点F,使得
上是否存在一点F,使得![]() 平面
平面![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,试说明理由;
的值;若不存在,试说明理由;
(2)在(1)的条件下,若![]() 与
与![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】线段AB为圆O的直径,点E,F在圆O上,AB//EF,矩形ABCD所在平面和圆O所在平面垂直,且![]() .则( )
.则( )
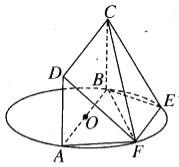
A.DF//平面BCE
B.异面直线BF与DC所成的角为30°
C.△EFC为直角三角形
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图被称为“中华第一图”,闪烁着中华文明进程的光辉,它是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相对统一的和谐美.定义:能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”,设圆O:![]() ,则下列说法中正确的是( )
,则下列说法中正确的是( )

A.函数![]() 是圆O的一个太极函数
是圆O的一个太极函数
B.圆O的所有非常数函数的太极函数都不能为偶函数
C.函数![]() 是圆O的一个太极函数
是圆O的一个太极函数
D.函数![]() 的图象关于原点对称是
的图象关于原点对称是![]() 为圆O的太极函数的充要条件
为圆O的太极函数的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点为坐标原点O,对称轴为![]() 轴,其准线为
轴,其准线为![]() .
.
(1)求抛物线C的方程;
(2)设直线![]() ,对任意的
,对任意的![]() 抛物线C上都存在四个点到直线l的距离为
抛物线C上都存在四个点到直线l的距离为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
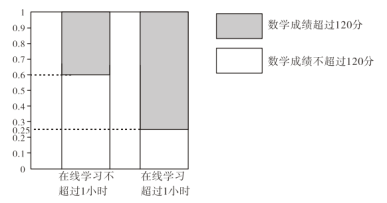
(Ⅰ)将频率视为概率,求学习时长不超过1小时但考试成绩超过120分的概率;
(Ⅱ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”.
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
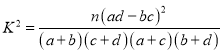
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com