
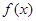 是定义在
是定义在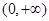 上的非负可导函数,且满足
上的非负可导函数,且满足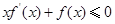 ,对任意正数
,对任意正数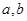 ,若
,若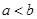 ,则必有( )
,则必有( )A.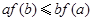 | B.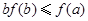 |
C.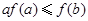 | D.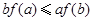 |
 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源:不详 题型:解答题
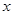 万件,需另投入流动成本为
万件,需另投入流动成本为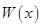 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,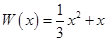 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,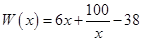 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.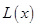 (万元)关于年产量
(万元)关于年产量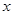 (万件)的函数解析式;
(万件)的函数解析式;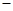 固定成本
固定成本 流动成本)
流动成本)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
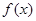 是定义在
是定义在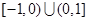 上的函数,当
上的函数,当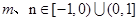 ,且
,且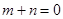 时,有
时,有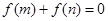 .
.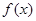 是奇函数;
是奇函数;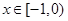 时,
时, (a为实数). 则当
(a为实数). 则当 时,求
时,求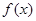 的解析式;
的解析式;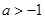 时,试判断
时,试判断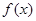 在
在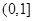 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com