
【题目】已知命题p:k2﹣8k﹣20≤0,命题q:方程 ![]() =1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
=1表示焦点在x轴上的双曲线. (Ⅰ)命题q为真命题,求实数k的取值范围;
(Ⅱ)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:
【题目】在斜三棱柱ABC﹣A1B1C1中BC⊥CC1 , AC=BC=2,A1在底面ABC上的射影恰为AC的中点D. 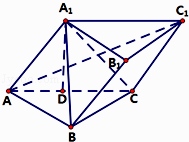
(1)证明:BC⊥平面ACC1A1
(2)若二面角A﹣A1B﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正三棱柱(底面是正三角形的直棱柱)ABC﹣A1B1C1中,已知AB=2,CC1= ![]() ,则异面直线AB1和BC1所成角的正弦值为( )
,则异面直线AB1和BC1所成角的正弦值为( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣
)﹣ ![]() sin2x+sinxcosx.
sin2x+sinxcosx.
(1)当x∈[0, ![]() ]时,求f(x)的值域;
]时,求f(x)的值域;
(2)用五点法在图中作出y=f(x)在闭区间[﹣ ![]() ,
, ![]() ]上的简图;
]上的简图;
(3)说明f(x)的图象可由y=sinx的图象经过怎样的变化得到? 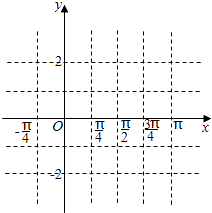
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|=
=1(a>b>0)的右焦点为F,右顶点、上顶点分别为点A、B,且|AB|= ![]() |BF|.
|BF|. 
(Ⅰ)求椭圆C的离心率;
(Ⅱ)若斜率为2的直线l过点(0,2),且l交椭圆C于P、Q两点,OP⊥OQ.求直线l的方程及椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=loga(x+2)﹣1(a>0,a≠1)的图象恒过定点A,若点A在直线mx+ny+1=0上,其中m>0,n>0,则 ![]() +
+ ![]() 的最小值为( )
的最小值为( )
A.3+2 ![]()
B.3+2 ![]()
C.7
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 其中M∪P=R,则下列结论中一定正确的是( )
其中M∪P=R,则下列结论中一定正确的是( )
A.函数f(x)一定存在最大值
B.函数f(x)一定存在最小值
C.函数f(x)一定不存在最大值
D.函数f(x)一定不存在最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com