练习册

  • 练习册
  • 试题
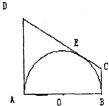
    精英家教网 > 高中数学 > 题目详情
    精英家教网如图，DA，CB，DC与以AB为直径的半圆分别相切于点A、B、E，且BC：AD=1：2，CD=3cm，则四边形ABCD的面积等于
     
    ．
    分析：根据三条线段与圆相切，知道从圆外一点做圆的切线，切线长相等，再根据两者的比值，得到两条切线的长度，根据勾股定理做出圆的直径，根据梯形的面积公式得到结果．
    解答：解：∵DA，CB，DC与以AB为直径的半圆分别相切于点A、B、E
    ∴DA=DE，CB=CE
    ∵BC：AD=1：2，CD=3cm
    ∴BC=1，AD=2，
    ∴圆的直径是
    		9-1
    =2
    		2
    ，
    ∴四边形的面积是
    (1+2)×2
    		2
    2
    =3
    		2

    故答案为：3
    		2
    点评：本题考查圆的切线的性质定理的证明，本题是一个典型的平面几何的求面积的题目，主要依据是圆的切线长之间的关系，运算量不大，是一个得分题目．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图（1）直线l∥AB，且与CA，CB分别相交于点E，F，EF与AB间的距离是d，点P是线段EF上任意一点，Q是线段AB上任意一点，则|PQ|的最小值等于d．类比上述结论我们可以得到：在图（2）中，平面α∥平面ABC，且与DA，DB，DC分别相交于点E，F，G，平面α与平面ABC间的距离是m，
    a，b分别是平面α与平面ABC内的任意一条直线，则a，b间距离的最小值是m．
    或P，Q分别是平面α与平面ABC内的任意一点，则P，Q间距离的最小值是m．
    a，b分别是平面α与平面ABC内的任意一条直线，则a，b间距离的最小值是m．
    或P，Q分别是平面α与平面ABC内的任意一点，则P，Q间距离的最小值是m．
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

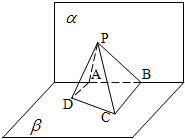    （2012•石景山区一模）如图，已知平面α∩β=l，A、B是l上的两个点，C、D在平面β内，且DA⊥α，CB⊥α，AD=4，AB=6，BC=8，在平面α上有一个动点P，使得∠APD=∠BPC，则P-ABCD体积的最大值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，甲站在水库底面上的点D处，乙站在水坝斜面上的点C处，已知测得从D、C到库底与水坝的交线的距离分别为DA=10
    		2
    米、CB=10米，AB的长为10米，CD的长为10
    		6
    米，则库底与水坝所成的二面角的大小为
    135
    135
     度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

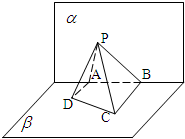    （2012•石景山区一模）如图，已知平面α∩β=l，A、B是l上的两个点，C、D在平面β内，且DA⊥α，CB⊥α，AD=4，AB=6，BC=8，在平面α上有一个动点P，使得∠APD=∠BPC，则△PAB面积的最大值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：阅读理解

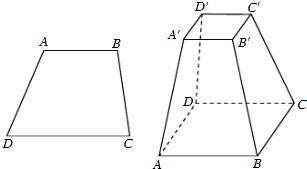    （必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
    方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
    设OE=x，∵△OAB∽△ODC，∴
    x
    x+h
    =
    a
    b
    ，即x=
    ah
    b-a
    ．
    ∴S梯形ABCD=S△ODC-S△OAB=
    1
    2
    b（x+h）-
    1
    2
    ax=
    1
    2
    （b-a）x+
    1
    2
    bh=
    1
    2
    （a+b）h．
    方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
    设梯形AMNB的高为x，MN=y，
    x
    h
    =
    y-a
    b-a
    ⇒y=a+
    b-a
    h
    x，∴S梯形ABCD=
    ∫
    h
    0
    （a+
    b-a
    h
    x）dx=（ax+
    b-a
    2h
    x2）
    |
    h
    0
    =ah+
    b-a
    2h
    •h2=
    1
    2
    （a+b）h．
    再解下面的问题：
    已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1，S2（S1＜S2），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=
    1
    3
    ×底面积×高）．

    查看答案和解析>>

    同步练习册答案