
【题目】已知椭圆C:![]() ,点P(0,1).
,点P(0,1).
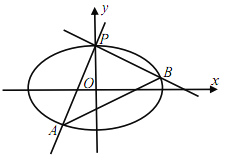
(1)过P点作斜率为k(k>0)的直线交椭圆C于A点,求弦长|PA|(用k表示);
(2)过点P作两条互相垂直的直线PA,PB,分别与椭圆交于A、B两点,试问:直线AB是否经过一定点?若存在,则求出定点,若不存在,则说明理由?
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】对于函数f(x),若存在x0∈R,使f(x0)=x0,则称x0是f(x)的一个不动点,已知f(x)=x2+ax+4在[1,3]恒有两个不同的不动点,则实数a的取值范围______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,当直线
两点,当直线![]() 过点
过点![]() 时,以
时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
(1)求抛物线![]() 的方程;
的方程;
(2)与![]() 平行的直线
平行的直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,若平行线
两点,若平行线![]() ,
,![]() 之间的距离为
之间的距离为![]() ,且
,且![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,求
倍,求![]() 和
和![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对任意![]() ,
,![]() ,
,![]() ,给出下列命题:
,给出下列命题:
①“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;
是无理数”的充要条件;
③“![]() ”是“
”是“![]() ”的必要条件,
”的必要条件,
④“![]() ”是“
”是“![]() ”的充分条件.
”的充分条件.
其中真命题的个数为().
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数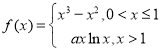 ,(
,(![]() ).
).
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设点![]() ,
,![]() 是函数
是函数![]() 图象的不同两点,其中
图象的不同两点,其中![]() ,
,![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,且函数
,且函数![]() 在点
在点![]() 切线的斜率为
切线的斜率为![]() ,若存在,请求出
,若存在,请求出![]() 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下,则一定符合该标志的是( )
甲地:中位数为2,极差为5; 乙地:总体平均数为2,众数为2;
丙地:总体平均数为1,总体方差大于0; 丁地:总体平均数为2,总体方差为3.
A.甲地B.乙地C.丙地D.丁地
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com