
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
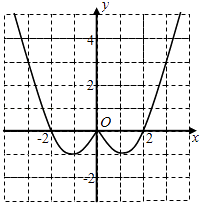
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间; 
(2)写出函数f(x)的解析式和值域.
【答案】
(1)解:因为函数为偶函数,故图象关于y轴对称,补出完整函数图象如有图:
所以f(x)的递增区间是(﹣1,0),(1,+∞)
(2)解:设x>0,则﹣x<0,所以f(﹣x)=x2﹣2x,因为f(x)是定义在R上的偶函数,所以f(﹣x)=f(x),所以x>0时,f(x)=x2﹣2x,
故f(x)的解析式为 ![]()
值域为{y|y≥﹣1}
【解析】(1)因为函数为偶函数,故图象关于y轴对称,由此补出完整函数f(x)的图象即可,再由图象直接可写出f(x)的增区间.(2)可由图象利用待定系数法求出x>0时的解析式,也可利用偶函数求解析式,值域可从图形直接观察得到.
【考点精析】关于本题考查的函数的值域和函数的单调性,需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +m为奇函数,m为常数.
+m为奇函数,m为常数.
(1)求实数m的值;
(2)判断并证明f(x)的单调性;
(3)若关于x的不等式f(f(x))+f(ma)<0有解,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB,☉O交直线OB于E,D两点,连接EC,CD. 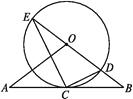
(1)求证:直线AB是☉O的切线;
(2)若tan∠CED= ![]() ,☉O的半径为3,求OA的长.
,☉O的半径为3,求OA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣ ![]()
(1)若f(x)是R上的奇函数,求m的值
(2)用定义证明f(x)在R上单调递增
(3)若f(x)值域为D,且D[﹣3,1],求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱长为a的正方体ABCD﹣A1B1C1D1中,点M,N,E分别是棱A1B1 , A1D1 , C1D1的中点. 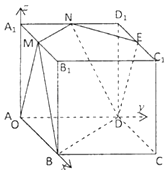
(1)过AM作一平面,使其与平面END平行(只写作法,不需要证明);
(2)在如图的空间直角坐标系中,求直线AM与平面BMND所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A=B=R,x∈A,y∈B,f:x→y=ax+b是从A到B的映射,若1和8的原象分别是3和10,则5在f下的象是( )
A.3
B.4
C.5
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com