
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数, ![]() ).
).
(1)求![]() 的单调区间和极值;
的单调区间和极值;
(2)求证:当![]() ,且
,且![]() 时,
时, ![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(Ⅰ)求出函数的导数,列出变化表,求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)问题等价于![]() , 设
, 设![]() , 根据函数的单调性证明即可.
, 根据函数的单调性证明即可.
试题解析:
(1)解 由f(x)=ex-3x+3a,x∈R知f′(x)=ex-3,x∈R.
令f′(x)=0,得x=ln 3,
于是当x变化时,f′(x),f(x)的变化情况如下表.
x | (-∞,ln 3) | ln 3 | (ln 3,+∞) |
f′(x) | - | 0 | + |
f(x) |
| 3(1-ln 3+a) |
|
故f(x)的单调递减区间是(-∞,ln 3],
单调递增区间是[ln3,+∞),
f(x)在x=ln 3处取得极小值,极小值为f(ln 3)=eln3-3ln 3+3a=3(1-ln 3+a).
(2)证明:待证不等式等价于![]()
设![]() ,x∈R,
,x∈R,
于是![]() ,x∈R.
,x∈R.
由(I)及![]() 知:
知: ![]() 的最小值为g′(ln 3)=3(1-ln 3+a)>0.
的最小值为g′(ln 3)=3(1-ln 3+a)>0.
于是对任意x∈R,都有![]() >0,所以g(x)在R内单调递增.
>0,所以g(x)在R内单调递增.
于是当![]() 时,对任意x∈(0,+∞),都有g(x)>g(0).
时,对任意x∈(0,+∞),都有g(x)>g(0).
而g(0)=0,从而对任意x∈(0,+∞),g(x)>0.
即![]() ,故
,故![]() .
.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣ ![]()
(1)若f(x)是R上的奇函数,求m的值
(2)用定义证明f(x)在R上单调递增
(3)若f(x)值域为D,且D[﹣3,1],求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别是a,b,c,已知2cosA(bcosC+ccosB)=a.
(1)求角A;
(2)若a= ![]() ,b+c=5,求△ABC的面积.
,b+c=5,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱长为a的正方体ABCD﹣A1B1C1D1中,点M,N,E分别是棱A1B1 , A1D1 , C1D1的中点. 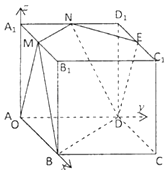
(1)过AM作一平面,使其与平面END平行(只写作法,不需要证明);
(2)在如图的空间直角坐标系中,求直线AM与平面BMND所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈[1,12],x2﹣a≥0.命题q:x0∈R,使得x02+(a﹣1)x0+1<0.若p或q为真,p且q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中实数
,其中实数![]() 为常数,
为常数,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,解关于
时,解关于![]() 的不等式
的不等式![]() ;
;
(3)当![]() 时,如果函数
时,如果函数![]() 不存在极值点,求
不存在极值点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆C1:x2+y2﹣6x+5=0相交于不同的两点A,B.
(1)求圆C1的圆心坐标;
(2)求线段AB 的中点M的轨迹C的方程;
(3)是否存在实数 k,使得直线L:y=k(x﹣4)与曲线 C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com