练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB⊥AD，，AC＝AD＝CD，E是AD的中点．

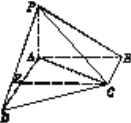
    (Ⅰ)证明CE∥平面PAB；

    (Ⅱ)证明：平面PAD⊥平面PCE.

    【答案】(Ⅰ)见解析(Ⅱ)见解析

    【解析】试题分析：（1）且，通过证明来证明CE∥平面PAB。（2）通过证明CE⊥平面PAD，可以证明平面PAD⊥平面PCE.

    试题解析：(Ⅰ)证明：∵AC＝AD＝CD，E是AD的中点，

    ∴CE⊥AD，又在平面ABCD内AB⊥AD，∴AB∥CE

    ∵CE平面PAB，AB平面PAB ∴CE∥平面PAB.

    (Ⅱ)证明：∵PA⊥平面ABCD ，CE平面ABCD，∴PA⊥CE.

    ∵AC＝AD＝CD，E是AD中点，∴AD⊥CE.

    ∵PA∩AD＝A，∴CE⊥平面PAD，

    ∵CE平面PCE ∴平面PAD⊥平面 PCE.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝sinωxcosωx－cos2ωx＋ (ω＞0)，经化简后利用“五点法”画其在某一周期内的图象时，列表并填入的部分数据如下表：

    x

    ①

    f(x)

    0

    1

    0

    －1

    0

    (1)请直接写出①处应填的值，并求函数f(x)在区间上的值域；

    (2)△ABC的内角A，B，C所对的边分别为a，b，c，已知f(A＋)＝1，b＋c＝4，a＝，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4－5：不等式选讲](10分)

    已知函数f(x)＝2|x－2|＋3|x＋3|.

    (Ⅰ)解不等式：f(x)>15；

    (Ⅱ)若函数f(x)的最小值为m，正实数a，b满足4a＋25b＝m，求＋的最小值，并求出此时a，b的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，平面五边形ABCDE中，AB∥CE，且AE＝2，∠AEC＝60°，CD＝ED＝，cos∠EDC＝.将△CDE沿CE折起，使点D移动到P的位置，且AP＝，得到四棱锥P－ABCE.

    (1)求证：AP⊥平面ABCE；

    (2)记平面PAB与平面PCE相交于直线l，求证：AB∥l.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 (其中e是自然对数的底数，k∈R)．

    (1)讨论函数的单调性；

    (2)当函数有两个零点时，证明： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)＝|x－1|＋|x－a|，a∈R.

    (Ⅰ)当a＝4时，求不等式f(x)≥7的解集；

    (Ⅱ)若f(x)≥5对x∈R恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥PABC中，不能证明AP⊥BC的条件是(　　)

    A. AP⊥PB，AP⊥PC

    B. AP⊥PB，BC⊥PB

    C. 平面BPC⊥平面APC，BC⊥PC

    D. AP⊥平面PBC

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设向量， ，记

    (1)求函数f(x)的最小正周期；

    (2)试用“五点法”画出函数f(x)在区间上的简图，并指出该函数的图象可由y＝sin x(x∈R)的图象经过怎样的平移和伸缩变换得到；

    (3)若函数g(x)＝f(x)＋m， 的最小值为2，试求出函数g(x)的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥PABCD的三视图如图所示，四棱锥PABCD的五个顶点都在一个球面上， E，F分别是棱AB，CD的中点，直线EF被球面所截得的线段长为2 ，则该球的表面积为

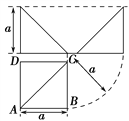
    A. 12π B. 24π C. 36π D. 48π

    查看答案和解析>>

    同步练习册答案