
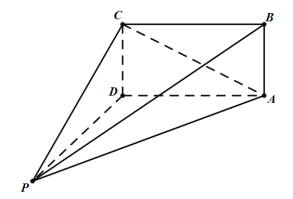
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 为正方形,且
为正方形,且![]() .若四棱锥
.若四棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,则球
的球面上,则球![]() 的表面积的最小值为_____;当四棱锥
的表面积的最小值为_____;当四棱锥![]() 的体积取得最大值时,二面角
的体积取得最大值时,二面角![]() 的正切值为_______.
的正切值为_______.
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】在![]() 年俄罗斯索契冬奥会某项目的选拔比赛中,
年俄罗斯索契冬奥会某项目的选拔比赛中,![]() 、
、![]() 两个代表队进行对抗赛,每队三名队员,
两个代表队进行对抗赛,每队三名队员,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,
,![]() 队队员是
队队员是![]() 、
、![]() 、
、![]() ,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得
,按以往多次比赛的统计,对阵队员之间胜负概率如下表,现按表中对阵方式出场进行三场比赛,每场胜队得![]() 分,负队得
分,负队得![]() 分,设
分,设![]() 队、
队、![]() 队最后所得总分分别为
队最后所得总分分别为![]() 、
、![]() 且
且![]() .
.
对阵队员 |
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 队得分为
队得分为![]() 分的概率;
分的概率;
(2)求![]() 的分布列;并用统计学的知识说明哪个队实力较强.
的分布列;并用统计学的知识说明哪个队实力较强.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=![]() ,.计划在
,.计划在![]() 上再建一座观赏亭P,记∠POB=θ
上再建一座观赏亭P,记∠POB=θ![]() .
.
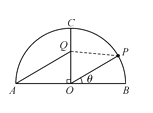
(1)当θ=![]() 时,求∠OPQ的大小;
时,求∠OPQ的大小;
(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,求游客在观赏亭P处的观赏效果最佳时,角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2010年4月1日—4月30日对空气污染指数的监测数据如(主要污染物为可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
样本频率分布表:
分组 | 频数 | 频率 |
[41,51) | 2 | |
[51,61) | 1 | |
[61,71) | 4 | |
[71,81) | 6 | |
[81,91) | 10 | |
[91,101) | ||
[101,111) | 2 |
(1) 完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且acosC=(2b﹣c)cosA.
(1)若![]() 3,求△ABC的面积;
3,求△ABC的面积;
(2)若∠B<∠C,求2cos2B+cos2C的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由我国引领的5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对![]() 增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
增长产生直接贡献,并通过产业间的关联效应和波及效应,间接带动国民经济各行业的发展,创造岀更多的经济增加值.如图是某单位结合近年数据,对今后几年的5G经济产出所做的预测.结合下图,下列说法正确的是( )
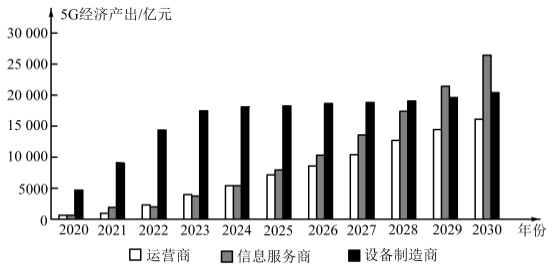
A.5G的发展带动今后几年的总经济产出逐年增加
B.设备制造商的经济产出前期增长较快,后期放缓
C.设备制造商在各年的总经济产出中一直处于领先地位
D.信息服务商与运营商的经济产出的差距有逐步拉大的趋势
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
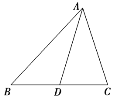
(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线T的焦点为F,准线为l,过F的直线m与T交于A,B两点,C,D分别为A,B在l上的射影,M为AB的中点,若m与l不平行,则△CMD是( )
A. 等腰三角形且为锐角三角形
B. 等腰三角形且为钝角三角形
C. 等腰直角三角形
D. 非等腰的直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
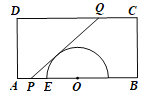
【题目】某生态农场有一矩形地块,地块内有一半圆形池塘(如图所示),其中![]() 百米,
百米,![]() 百米,半圆形池塘的半径为1百米,圆心
百米,半圆形池塘的半径为1百米,圆心![]() 与线段
与线段![]() 的中点重合,半圆与
的中点重合,半圆与![]() 的左侧交点为
的左侧交点为![]() .该农场计划分别在
.该农场计划分别在![]() 和
和![]() 上各选一点
上各选一点![]() ,修建道路
,修建道路![]() ,要求
,要求![]() 与半圆相切.
与半圆相切.
(1)若![]() ,求该道路的总长;
,求该道路的总长;
(2)若![]() 为观光道路,修建费用是4万元/百米,
为观光道路,修建费用是4万元/百米,![]() 为便道,修建费用是1万元/百米,求修建观光道路与便道的总费用的最小值.
为便道,修建费用是1万元/百米,求修建观光道路与便道的总费用的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com