
已知函数 ,其中常数
,其中常数 满足
满足
(1)若 ,判断函数
,判断函数 的单调性;
的单调性;
(2)若 ,求
,求 时的
时的 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
某地区注重生态环境建设,每年用于改造生态环境总费用为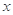 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少
亿元。该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.
亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.
若 ,
,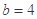 ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y= 作为生态环境改造投资方案.
作为生态环境改造投资方案.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=loga(x+1)-loga(1-x)(a>0,a≠1)
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性,并给出证明;
(3)当a>1时,求使f(x)>0的x的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com