
【题目】已知:{an}是公比大于1的等比数列,Sn为其前n项和,S3=7,且a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项公式;
(2)令bn=log2a3n+1,求数列{bn}的前n项和Tn.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 、
、![]() 为椭圆的左、右焦点,
为椭圆的左、右焦点,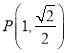 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆的标准方程;
(2)设直线![]() ,过点
,过点![]() 的直线交椭圆于
的直线交椭圆于![]() 、
、![]() 两点,线段
两点,线段![]() 的垂直平分线分别交直线
的垂直平分线分别交直线![]() 、直线
、直线![]() 于
于![]() 、
、![]() 两点,当
两点,当![]() 最小时,求直线
最小时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节是中国传统节日之一节日期间,各大商场各种品牌的“粽子战”便悄然打响.某记者走访市场发现,各大商场粽子种类繁多,价格不一根据数据统计分析,得到了某商场不同种类的粽子销售价格(单位:元/千克)的频数分布表,如表一所示.
表一:
价格/(元/千克) | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) |
种类数 | 4 | 12 | 16 | 6 | 2 |
在调查中,记者还发现,各大品牌在馅料方面还做足了功课,满足了市民多样化的需求除了蜜枣、豆沙等传统馅料粽,很多品牌还推出了鲜肉、巧克力、海鲜等特色馅料粽在该商场内,记者随机对100名顾客的年龄和粽子口味偏好进行了调查,结果如表二.
表二:
喜欢传统馅料粽 | 喜欢特色馅料粽 | 总计 | |
40岁以下 | 30 | 15 | 45 |
40岁及以上 | 50 | 5 | 55 |
总计 | 80 | 20 | 100 |
(1)根据表一估计该商场粽子的平均销售价(同一组中的数据用该组区间的中点值代表);
(2)根据表二信息能否有95%的把握认为顾客的粽子口味偏好与年龄有关?
参考公式和数据: (其中
(其中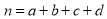 为样本容量)
为样本容量)
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() 相邻对称轴之间的距离为
相邻对称轴之间的距离为![]() ,且函数
,且函数![]() 在
在![]() 处取得最大值,则下列命题正确的个数为( )
处取得最大值,则下列命题正确的个数为( )
①当![]() 时,m的取值范围是
时,m的取值范围是 ;②将
;②将![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数为偶函数;③函数
个单位后所对应的函数为偶函数;③函数![]() 的最小正周期为
的最小正周期为![]() ;④函数
;④函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且椭圆
,且椭圆![]() 的一个顶点
的一个顶点![]() 的坐标为
的坐标为![]() .过椭圆
.过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() (
(![]() ,
,![]() 不同于点
不同于点![]() ),直线
),直线![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() .连接
.连接![]() ,过点
,过点![]() 作
作![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() .
.
(1)求椭圆![]() 的方程,并求点
的方程,并求点![]() 的坐标;
的坐标;
(2)求证:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“公平正义”是社会主义和谐社会的重要特征,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自已能否被录取?能获得什么样的职位? 某单位准备通过考试(按照高分优先录取的原则)录用![]() 名,其中
名,其中![]() 个高薪职位和
个高薪职位和![]() 个普薪职位.实际报名人数为
个普薪职位.实际报名人数为![]() 名,考试满分为
名,考试满分为![]() 分.(一般地,对于一次成功的考试来说,考试成绩应服从正态分布. )考试后考试成绩的部分统计结果如下:
分.(一般地,对于一次成功的考试来说,考试成绩应服从正态分布. )考试后考试成绩的部分统计结果如下:
考试平均成绩是![]() 分,
分,![]() 分及其以上的高分考生
分及其以上的高分考生![]() 名.
名.
(1)最低录取分数是多少?(结果保留为整数)
(2)考生甲的成绩为![]() 分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
分,若甲被录取,能否获得高薪职位?若不能被录取,请说明理由.
参考资料:(1)当![]() 时,令
时,令![]() ,则
,则![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,
中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置(
的位置(![]() 平面
平面![]() ).
).
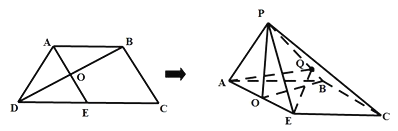
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,试判断线段
,试判断线段![]() 上是否存在一点
上是否存在一点![]() (不含端点),使得直线
(不含端点),使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com