练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】甲、乙两名篮球运动员，甲投篮一次命中的概率为，乙投篮一次命中的概率为，若甲、乙各投篮三次，设为甲、乙投篮命中的次数的差的绝对值，其中甲、乙两人投篮是否命中相互没有影响.

    （1）若甲、乙第一次投篮都命中，求甲获胜（甲投篮命中数比乙多）的概率；

    （2）求的分布列及数学期望.

    【答案】（1）；（2）分布列见解析，1

    【解析】

    （1）甲获胜的情况为3:1,3:2,2:1分别计算概率即可得解；

    （2）的所有可能取值是0，1，2，3，分别计算概率，写出分布列，计算数学期望.

    （1）甲以3:1获胜的概率，

    甲以3:2获胜的概率，

    甲以2:1获胜的概率，

    则甲获胜的概率

    （2）由题意可得的所有可能取值是0，1，2，3.

    ；

    ；

    ；

    .

    的分布列为

    0

    1

    2

    3

    故

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一个生产公司投资A生产线500万元，每万元可创造利润万元，该公司通过引进先进技术，在生产线A投资减少了x万元，且每万元的利润提高了；若将少用的x万元全部投入B生产线，每万元创造的利润为万元，其中．

    若技术改进后A生产线的利润不低于原来A生产线的利润，求x的取值范围；

    若生产线B的利润始终不高于技术改进后生产线A的利润，求a的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合，若A∩B=B，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知

    （1）若函数在区间上单调递减，求实数的取值范围；

    （2）函数有几个零点？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在[e，+∞）上的函数f（x）满足f（x）+xlnxf′（x）＜0且f（2018）＝0，其中f′（x）是函数的导函数，e是自然对数的底数，则不等式f（x）＞0的解集为（　　）

    A. [e，2018） B. [2018，+∞） C. （e，+∞） D. [e，e+1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（， ）.

    （1）如果曲线在点处的切线方程为，求， 的值；

    （2）若， ，关于的不等式的整数解有且只有一个，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥，平面，且，底面为直角梯形，，，，，，，、分别为、的中点，平面与的交点为.

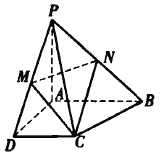
    （1）求的长度；

    （2）求截面的底面所成二面角的大小；

    （3）求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（2015秋运城期中）已知函数f（x）=（log2x﹣2）（log4x﹣）．

    （1）当x∈[1，4]时，求该函数的值域；

    （2）若f（x）≤mlog2x对于x∈[4，16]恒成立，求m得取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    在直角坐标系中，曲线的参数方程为（为参数），以原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （1）写出曲线的普通方程和曲线的直角坐标方程；

    （2）已知点是曲线上的动点，求点到曲线的最小距离．

    查看答案和解析>>

    同步练习册答案