
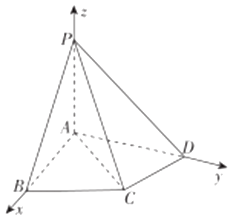
【题目】如图,在四棱锥P﹣ABCD中,△ABC为正三角形,AB⊥AD,AC⊥CD,PC= ![]() AC,平面PAC⊥平面ABCD.
AC,平面PAC⊥平面ABCD. 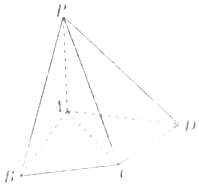
(1)点E在棱PC上,试确定点E的位置,使得PD⊥平面ABE;
(2)求二面角A﹣PD﹣C的余弦值.
【答案】
(1)解:∵ ![]() ,∴PA⊥AC,
,∴PA⊥AC,
又∵平面PAC⊥平面ABCD,平面PAC∩平面ABCD=AC,
∴PA⊥平面ABCD,可得PA⊥AB,PA⊥AD,又AB⊥AD,
以A为坐标原点,射线AB,AD,AP分别为x,y,z轴的正方向建立空间直角坐标系,
设PA=2,则 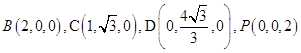 ,
,
∵ 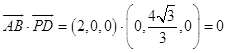 ,∴PD⊥AB.
,∴PD⊥AB.
设 ![]() ,
,
若AE⊥PD,则 ![]() ,即
,即 ![]() ,
,
即﹣4+λ8=0,得 ![]() ,即当E为PC的中点时,AE⊥PD,
,即当E为PC的中点时,AE⊥PD,
则PD⊥平面ABE,
∴当E为PC的中点时PD⊥平面ABE
(2)解:设平面PCD的一个法向量 ![]() =(x,y,z),
=(x,y,z), ![]()
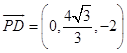 ,
,
则 ![]() 且
且 ![]() ,
,
即 ![]() 且
且 ![]() ,令
,令 ![]() ,则z=2,x=1,则
,则z=2,x=1,则 ![]() ,
,
再取平面PAD的一个法向量为 ![]() =(1,0,0).
=(1,0,0).
则cos< ![]() >=
>= ![]() =
= ![]() ,
,
故二面角A﹣PD﹣C的余弦值为 ![]() .
.
【解析】由已知可得PA⊥AC,结合面面垂直的性质可得PA⊥AB,PA⊥AD,以A为坐标原点,射线AB,AD,AP分别为x,y,z轴的正方向建立空间直角坐标系,求出所用点的坐标.(1)由数量积为0可得PD⊥AB,设 ![]() ,再由
,再由 ![]() 求得λ值,则点E的位置确定;(2)求出平面PCD的一个法向量,取平面PAD的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PD﹣C的余弦值.
求得λ值,则点E的位置确定;(2)求出平面PCD的一个法向量,取平面PAD的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PD﹣C的余弦值.
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),其中a为实数.
(Ⅰ)讨论并求出f(x)的极值;
(Ⅱ)在a<1时,是否存在m>1,使得对任意的x∈(1,m)恒有f(x)>0,并说明理由;
(Ⅲ) 确定a的可能取值,使得存在n>1,对任意的x∈(1,n),恒有|f(x)|<(x﹣1)2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的奇函数f(x)满足f(4﹣x)+f(x)=0,当﹣2<x<0时,f(x)=2x , 则f(log220)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,g(x)=
,g(x)=![]() ,若函数y=f(g(x))+a有三个不同的零点x1,x2,x3(其中x1<x2<x3),则2g(x1)+g(x2)+g(x3)的取值范围为______.
,若函数y=f(g(x))+a有三个不同的零点x1,x2,x3(其中x1<x2<x3),则2g(x1)+g(x2)+g(x3)的取值范围为______.
【答案】![]()
【解析】
首先研究函数![]() 和函数
和函数![]() 的性质,然后结合韦达定理和函数的性质求解2g(x1)+g(x2)+g(x3)的取值范围即可.
的性质,然后结合韦达定理和函数的性质求解2g(x1)+g(x2)+g(x3)的取值范围即可.
由题意可知:![]() ,
,
将对勾函数![]() 的图象向右平移一个单位,再向上平移一个单位即可得到函数
的图象向右平移一个单位,再向上平移一个单位即可得到函数![]() 的图象,其图象如图所示:
的图象,其图象如图所示:
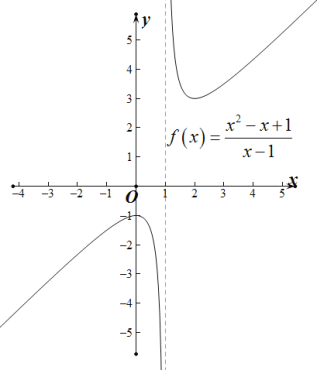
由![]() 可得
可得![]() ,
,
据此可知![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
绘制函数图象如图所示:
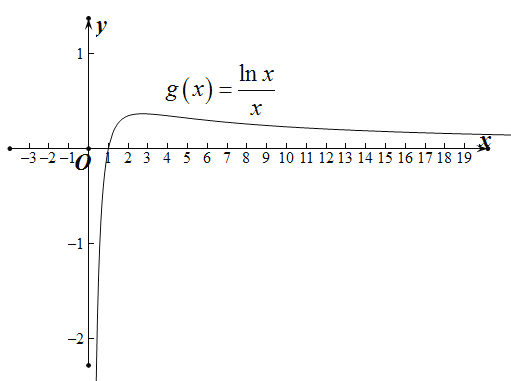
则![]() 的最大值为
的最大值为![]() ,
,![]() ,
,
函数y=f(g(x))+a有三个不同的零点,则![]() ,
,
令![]() ,则
,则![]() ,
,
整理可得:![]() ,由韦达定理有:
,由韦达定理有:![]() .
.
满足题意时,应有:![]() ,
,![]() ,
,
故![]() .
.
【点睛】
本题主要考查导数研究函数的性质,等价转化的数学思想,复合函数的性质及其应用等知识,意在考查学生的转化能力和计算求解能力.
【题型】填空题
【结束】
17
【题目】已知等比数列{![]() }的前n项和为
}的前n项和为![]() ,且满足2
,且满足2![]() =
=![]() +m(m∈R).
+m(m∈R).
(Ⅰ)求数列{![]() }的通项公式;
}的通项公式;
(Ⅱ)若数列{![]() }满足
}满足![]() ,求数列{
,求数列{![]() }的前n项和
}的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时![]() 的浓度;(II)规定:当一天内
的浓度;(II)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有6个人排成一排照相,由于甲乙性格不合,所以要求甲乙不相邻,丙最高,要求丙站在最中间的两个位置中的一个位置上,则不同的站法有( )种.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+(﹣1)n ![]() ,其中n∈N* , a为常数.
,其中n∈N* , a为常数.
(Ⅰ)当n=2,且a>0时,判断函数f(x)是否存在极值,若存在,求出极值点;若不存在,说明理由;
(Ⅱ)若a=1,对任意的正整数n,当x≥1时,求证:f(x+1)≤x.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2+bx+1在点(1,f(1))处的切线方程为4x﹣y﹣12=0.
(1)求函数f(x)的解析式;
(2)求f(x)的单调区间和极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com