
【题目】已知函数![]() .
.
(1)若![]() 存在最大值
存在最大值![]() ,证明:
,证明:![]() ;
;
(2)函数![]() ,且
,且![]() 只有一个极值点
只有一个极值点![]() ,求
,求![]() 的取值范围,并证明:
的取值范围,并证明:![]()
【答案】(1) 证明见解析(2) ![]() ,证明见解析
,证明见解析
【解析】
(1)先求函数![]() 的导数,分
的导数,分![]() 的范围讨论函数是否有最大值,并且在有最大值时根据函数的单调性求
的范围讨论函数是否有最大值,并且在有最大值时根据函数的单调性求![]() (a)
(a)![]() 的最小值等于零即可;
的最小值等于零即可;
(2)求函数![]() 的导数,且
的导数,且![]() 只有一个根,且定义域内根的两边区间的符合相反,求出根
只有一个根,且定义域内根的两边区间的符合相反,求出根![]() ,并证明
,并证明![]() 的最小值大于等于
的最小值大于等于![]() 即可.
即可.
解:(1)由题意:![]() ,
,
当![]() 时,
时,![]() 恒成立,函数
恒成立,函数![]() 单调递增,无最大值;
单调递增,无最大值;
当![]() ,
,![]() 在
在![]() 单调递增,
单调递增,![]() ,
,![]() 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 最大值为
最大值为![]() ,
,
所以![]() ,
,
下面证明![]() ,即证:
,即证:![]() ,令
,令![]() ,
, ![]() ,
,
所以![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
所以![]() ,所以
,所以![]() ,证毕.
,证毕.
(2)![]() ,所以
,所以![]() ,设
,设![]() ,
,![]() ,
,
①当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,
,![]() 单调递增,
单调递增,![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
若![]() ,
,![]() 恒成立,
恒成立,![]() 无极值;
无极值;
若![]() ,
,![]() ,而
,而![]() ,
,![]() ,此时函数
,此时函数![]() 有两个极值点:
有两个极值点:
故![]() 不符合题意
不符合题意
②![]() 时,
时,![]() ,
,![]() ,
,![]() 单调递减,
单调递减,![]() ,
,![]() ,
,![]() 单调递增,
单调递增,
所以函数![]() 有唯一的极小值点
有唯一的极小值点![]() ,
,![]() ;
;
③当![]() ,
,![]() 恒成立,
恒成立,![]() 单调递增,取
单调递增,取![]() 满足
满足![]() ,且
,且![]() 时,
时,![]() ,而
,而![]() ,此时又零点存在定理知:
,此时又零点存在定理知:![]() 有唯一的零点
有唯一的零点![]() ,
,![]() 只有一个极值点
只有一个极值点![]() ,且
,且![]() ,由题知
,由题知![]() ,又
,又![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,当
,当![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,
![]() 成立,
成立,
综上:函数![]() 只有一个极值点
只有一个极值点![]() 取值范围
取值范围![]() ,
,![]() ,且
,且![]() .
.


科目:高中数学 来源: 题型:
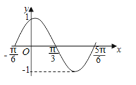
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() 的图象上的所有点( )
的图象上的所有点( )
A.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为a,∠D=60°,点H为DC边中点,现以线段AH为折痕将△DAH折起使得点D到达点P的位置且平面PHA⊥平面ABCH,点E,F分别为AB,AP的中点.
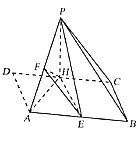
(1)求证:平面PBC∥平面EFH;
(2)若三棱锥P﹣EFH的体积等于![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() ,满足
,满足![]() .
.
(1)若![]() ,求数列前10项和;
,求数列前10项和;
(2)若![]() ,且数列
,且数列![]() 前2017项中有100项是0,求
前2017项中有100项是0,求![]() 的可能值;
的可能值;
(3)求证:在数列![]() 中,存在
中,存在![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
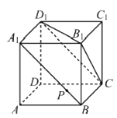
【题目】如图,在正方体![]() 中,点
中,点![]() 在线段
在线段![]() 上移动,有下列判断:①平面
上移动,有下列判断:①平面![]() 平面
平面![]() ;②平面
;②平面![]() 平面
平面![]() ;③三棱锥
;③三棱锥![]() 的体积不变;④
的体积不变;④![]() 平面
平面![]() .其中,正确的是______.(把所有正确的判断的序号都填上)
.其中,正确的是______.(把所有正确的判断的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)已知m+n=1(m,n>0),若|x-a|-f(x)≤![]() (a>0)恒成立,求实数a的取值范围.
(a>0)恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com