
 有最大值4
有最大值4
 有最大值
有最大值
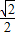
 =
= =2+
=2+ ≥4,故A不正确.
≥4,故A不正确. ,可得 ab≤
,可得 ab≤ ,故B不正确.
,故B不正确. =1+2
=1+2 ≤2,故
≤2,故  ≤
≤ ,故 C 正确.
,故 C 正确. =
= ,故D不正确.
,故D不正确.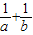 =
= =2+
=2+ ≥2+2=4,故
≥2+2=4,故 有最小值4,故A不正确.
有最小值4,故A不正确. ,∴ab≤
,∴ab≤ ,故ab有最大值
,故ab有最大值 ,故B不正确.
,故B不正确. =a+b+2
=a+b+2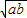 =1+2
=1+2 ≤2,∴
≤2,∴ ≤
≤ ,故
,故 有最大值为
有最大值为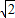 ,故C正确.
,故C正确. =
= ,故a2+b2有最小值
,故a2+b2有最小值 ,故D不正确.
,故D不正确.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com