
ЁОЬтФПЁПОнРњЪЗМЧдиЃЌУРШедкжаЭОЕК(Midway)КЃеНЧАЃЌУРЗННиЛёСЫШеЗНУмТыЕчБЈЃЌОнУРЗНвбЦЦвыЕФУмТыЕУжЊЃЌШеЗННЋЯђФГЕКНјааОќЪТЛюЖЏЃЌЕЋЙиМќКЌгаЕиЕуЕФВПЗжШДБЛШеЗНЛЛГЩСЫСэвЛжжУмТыЃЎОзЈМвбаОПЃЌЙРМЦЪЧвЛжжУмГзУмТыЃЌЧвУмГзЮЊ3ЮЛЃЎЫљЮНУмГзУмТыЪЧжИЃКНЋвЛЖЮгЂЮФзжФИЕФУїЮФ(ЮДМгУмЧАдЮФ)ОЙ§ЖдФГвЛзщЪ§зж(МДУмГз)ЕФБфЛЛЃЌИФБфГЩСЫСэвЛзщгЂЮФзжФИГЩЮЊУмЮФ(МгУмКѓЕФЮФзж)Р§ШчЃКУїЮФЃК![]() (ВЛМЦПеИёЃЌВЛМЦДѓаЁаД)дкУмГзЮЊЃК1 9 2ЕФЬѕМўЯТЃЌБфЛЛЙ§ГЬШчЯТЭМЫљЪОЃК
(ВЛМЦПеИёЃЌВЛМЦДѓаЁаД)дкУмГзЮЊЃК1 9 2ЕФЬѕМўЯТЃЌБфЛЛЙ§ГЬШчЯТЭМЫљЪОЃК
s | t | u | d | e | n | t |
1 | 9 | 2 | 1 | 9 | 2 | 1 |
t | c | w | e | n | p | u |
дђУмЮФЮЊЃК![]() ЃЌЪдИљОнЩЯУцаХЯЂЛиД№ЯТУцЮЪЬтЃК
ЃЌЪдИљОнЩЯУцаХЯЂЛиД№ЯТУцЮЪЬтЃК
ЃЈ1ЃЉдкУмГзЮЊ111ЕФЬѕМўЯТЃЌЬюаДЯТБэЃЌВЂаДГіУмЮФЃЛ
s | t | u | d | e | n | t |
УмЮФ____________________ЃЎ
ЃЈ2ЃЉШє![]()
![]() ЧыЬюаДЯТБэЃЌВЂаДГіУмГзЃЛ
ЧыЬюаДЯТБэЃЌВЂаДГіУмГзЃЛ
s | t | u | d | e | n | t |
УмГзЮЊ_____________ЃЎ
ЃЈ3)ШєЯТУцМДЪЧФЧЖЮАќКЌЕиЕу(Midway)ЕФЦЦвыВЛГіЕФУмЮФЃК![]() ,ЧвДЫЖЮУмЮФвВЪЧ3ЮЛУмГзМгУмЃЌЪдЬюаДЯТБэЃЌаДГіУмГзЃЌВЂНЋДЫЖЮУмЮФЗвыГЩУїЮФЃЎЃЈВЛБижЄУїЃЌаДГіУїЮФМДПЩЃЉ
,ЧвДЫЖЮУмЮФвВЪЧ3ЮЛУмГзМгУмЃЌЪдЬюаДЯТБэЃЌаДГіУмГзЃЌВЂНЋДЫЖЮУмЮФЗвыГЩУїЮФЃЎЃЈВЛБижЄУїЃЌаДГіУїЮФМДПЩЃЉ
c | w | b | c | f | s | o | l | l | y | d | g |
УмГзЮЊ___________ЃЌУїЮФЮЊ_________ЃЎ
ЁОД№АИЁПЃЈ1ЃЉБэМћНтЮіЃЌtuvefou ЃЈ2ЃЉБэМћНтЮіЃЛУмГзЮЊЃК123ЁЃЃЈ3ЃЉБэМћНтЮіЃЌУмГзЮЊЃК238ЃЌУїЮФЮЊЃК![]() ЁЃ
ЁЃ
ЁОНтЮіЁП
ИљОнвбжЊЬѕМўжЊЃКУїЮФЁА![]() ЁБОЙ§УмГзЁА192ЁБЕФБфЛЛЕУУмЮФЁА
ЁБОЙ§УмГзЁА192ЁБЕФБфЛЛЕУУмЮФЁА![]() ЁБЕФЙцдђЪЧЃКУїЮФжаЕФгЂЮФзжФИАДгЂЮФзжФИБэжаЕФзжФИЫГађЃЌвРДЮАДУмГзЁА192ЁБЖдгІЕФЪ§зжвЦЖЏЯргІИіЕФЮЛжУКѓЫљЕУЕФгЂЮФзжФИОЭЪЧУмЮФжаЫљЖдгІЕФзжФИЃЌШчЃКЁАsЁБЖдгІЕФЪ§бЇЪЧЁА1ЁБЃЌЫљвддкЁАsЁБЕФЮЛжУЯђгввЦЖЏ1ИіЮЛжУЃЌЫљЖдгІЕФзжФИЪЧЁАtЁБЃЌдйШчЃКЁАtЁБЖдгІЕФЪ§бЇЪЧЁА9ЁБЃЌЫљвддкЁАtЁБЕФЮЛжУЯђгввЦЖЏ9ИіЮЛжУЃЌЫљЖдгІЕФзжФИЪЧЁАcЁБЃЌ
ЁБЕФЙцдђЪЧЃКУїЮФжаЕФгЂЮФзжФИАДгЂЮФзжФИБэжаЕФзжФИЫГађЃЌвРДЮАДУмГзЁА192ЁБЖдгІЕФЪ§зжвЦЖЏЯргІИіЕФЮЛжУКѓЫљЕУЕФгЂЮФзжФИОЭЪЧУмЮФжаЫљЖдгІЕФзжФИЃЌШчЃКЁАsЁБЖдгІЕФЪ§бЇЪЧЁА1ЁБЃЌЫљвддкЁАsЁБЕФЮЛжУЯђгввЦЖЏ1ИіЮЛжУЃЌЫљЖдгІЕФзжФИЪЧЁАtЁБЃЌдйШчЃКЁАtЁБЖдгІЕФЪ§бЇЪЧЁА9ЁБЃЌЫљвддкЁАtЁБЕФЮЛжУЯђгввЦЖЏ9ИіЮЛжУЃЌЫљЖдгІЕФзжФИЪЧЁАcЁБЃЌ
ЃЈ1ЃЉАДгЂЮФзжФИБэЕФзжФИЫГађЃЌвРДЮШЁЁА![]() ЁБжаЕФзжФИЫљдкЕФЮЛжУЯђгввЦЖЏ1ИіЮЛжУКѓЫљдкЕФзжФИОЭЪЧЫљЖдгІЕФУмЮФЃЛ
ЁБжаЕФзжФИЫљдкЕФЮЛжУЯђгввЦЖЏ1ИіЮЛжУКѓЫљдкЕФзжФИОЭЪЧЫљЖдгІЕФУмЮФЃЛ
ЃЈ2ЃЉ![]()
![]() ИљОнгЂЮФзжФИЫГађБэЕУзжФИЁАsЁБЕНзжФИЁАtЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌзжФИЁАtЁБЕНзжФИЁАvЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌзжФИЁАuЁБЕНзжФИЁАxЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌПЩЕУУмГзЃЛ
ИљОнгЂЮФзжФИЫГађБэЕУзжФИЁАsЁБЕНзжФИЁАtЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌзжФИЁАtЁБЕНзжФИЁАvЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌзжФИЁАuЁБЕНзжФИЁАxЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌПЩЕУУмГзЃЛ
ЃЈ3ЃЉгЩгкУмГзЪЧ3ЮЛЪ§зжЃЌЫљвдУмЮФЁА![]() ЁБжазжФИЁА
ЁБжазжФИЁА![]() ЁБЁЂЁА
ЁБЁЂЁА![]() ЁБ
ЁБ![]() вРДЮЯђзѓвЦЖЏЕФЮЛжУЪ§ЪЧвЛбљЕФЃЌПЩвдЭЦГіУїЮФКЭУмГз.
вРДЮЯђзѓвЦЖЏЕФЮЛжУЪ§ЪЧвЛбљЕФЃЌПЩвдЭЦГіУїЮФКЭУмГз.
ЃЈ1ЃЉАДгЂЮФзжФИБэЕФзжФИЫГађЃЌвРДЮШЁЁА![]() ЁБжаЕФзжФИЫљдкЕФЮЛжУЯђгввЦЖЏ1ИіЮЛжУКѓЫљдкЕФзжФИОЭЪЧЫљЖдгІЕФУмЮФЃЌМћШчЯТЕФБэИёЃК
ЁБжаЕФзжФИЫљдкЕФЮЛжУЯђгввЦЖЏ1ИіЮЛжУКѓЫљдкЕФзжФИОЭЪЧЫљЖдгІЕФУмЮФЃЌМћШчЯТЕФБэИёЃК
s | t | u | d | e | n | t |
1 | 1 | 1 | 1 | 1 | 1 | 1 |
t | u | v | e | f | o | u |
УмЮФЮЊЃКtuvefou
ЃЈ2ЃЉ![]()
![]() ИљОнгЂЮФзжФИЫГађБэЕУзжФИЁАsЁБЕНзжФИЁАtЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌзжФИЁАtЁБЕНзжФИЁАvЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌзжФИЁАuЁБЕНзжФИЁАxЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌПЩЕУУмГзЮЊЃК123.
ИљОнгЂЮФзжФИЫГађБэЕУзжФИЁАsЁБЕНзжФИЁАtЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌзжФИЁАtЁБЕНзжФИЁАvЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌзжФИЁАuЁБЕНзжФИЁАxЁБашвЊвЦЖЏЕФЮЛжУЪ§ЃЌПЩЕУУмГзЮЊЃК123.
s | t | u | d | e | n | t |
1 | 2 | 3 | 1 | 2 | 3 | 1 |
t | v | x | e | g | q | u |
УмГзЮЊЃК123ЁЃ
ЃЈ3) гЩгкУмГзЪЧ3ЮЛЪ§зжЃЌЫљвдУмЮФЁА![]() ЁБжазжФИЁА
ЁБжазжФИЁА![]() ЁБЁЂЁА
ЁБЁЂЁА![]() ЁБ
ЁБ![]() вРДЮЯђзѓвЦЖЏЕФЮЛжУЪ§ЪЧвЛбљЕФЃЌПЩвдЭЦГіУїЮФЮЊ
вРДЮЯђзѓвЦЖЏЕФЮЛжУЪ§ЪЧвЛбљЕФЃЌПЩвдЭЦГіУїЮФЮЊ![]() КЭУмГзЮЊ238.
КЭУмГзЮЊ238.
a | t | t | a | c | n | m | i | d | w | a | y |
2 | 3 | 8 | 2 | 3 | 8 | 2 | 3 | 8 | 2 | 3 | 8 |
c | w | b | c | f | s | o | l | l | y | d | g |
УмГзЮЊЃК238ЃЌУїЮФЮЊЃК![]() ЁЃ
ЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЖЈвхдк![]() ЩЯЕФКЏЪ§
ЩЯЕФКЏЪ§![]() ЃЌгаЯТЪіУќЬтЃКЂйШє
ЃЌгаЯТЪіУќЬтЃКЂйШє![]() ЪЧЦцКЏЪ§ЃЌдђ
ЪЧЦцКЏЪ§ЃЌдђ![]() ЕФЭМЯѓЙигкЕу
ЕФЭМЯѓЙигкЕу![]() ЖдГЦЃЛЂкКЏЪ§
ЖдГЦЃЛЂкКЏЪ§![]() ЕФЭМЯѓЙигкжБЯп
ЕФЭМЯѓЙигкжБЯп![]() ЖдГЦЃЌдђ
ЖдГЦЃЌдђ![]() ЮЊХМКЏЪ§ЃЛЂлШєЖд
ЮЊХМКЏЪ§ЃЛЂлШєЖд![]() ЃЌга
ЃЌга![]() ЃЌдђ2ЪЧ
ЃЌдђ2ЪЧ![]() ЕФвЛИіжмЦкЃЛЂмКЏЪ§
ЕФвЛИіжмЦкЃЛЂмКЏЪ§![]() гы
гы![]() ЕФЭМЯѓЙигкжБЯп
ЕФЭМЯѓЙигкжБЯп![]() ЖдГЦ.Цфжае§ШЗЕФУќЬтЪЧ______.ЃЈаДГіЫљгае§ШЗУќЬтЕФађКХЃЉ
ЖдГЦ.Цфжае§ШЗЕФУќЬтЪЧ______.ЃЈаДГіЫљгае§ШЗУќЬтЕФађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖ![]() жаЃЌ
жаЃЌ![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЎ
ЕФжаЕуЃЎ
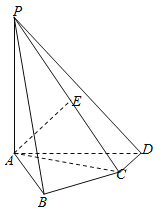
ЃЈ1ЃЉЧѓ![]() КЭЦНУц
КЭЦНУц![]() ЫљГЩЕФНЧЕФДѓаЁЃЎ
ЫљГЩЕФНЧЕФДѓаЁЃЎ
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФе§ЯвжЕЃЎ
ЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊЭждВ
жаЃЌвбжЊЭждВ![]() Й§Еу
Й§Еу![]() ЃЌЧвРыаФТЪ
ЃЌЧвРыаФТЪ![]() .
.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉжБЯп![]() ЕФаБТЪЮЊ
ЕФаБТЪЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыЭждВ
гыЭждВ![]() НЛгк
НЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФУцЛ§ЕФзюДѓжЕ.
ЕФУцЛ§ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЪЧЪРНчЩЯбЯжиШБЫЎЕФЙњМвЃЌФГЪаЮЊСЫжЦЖЈКЯРэЕФНкЫЎЗНАИЃЌЖдОгУёгУЫЎЧщПіНјааЕїВщЃЌЭЈЙ§ГщбљЃЌЛёЕУФГФъ100ЮЊОгУёУПШЫЕФдТОљгУЫЎСПЃЈЕЅЮЛЃКЖжЃЉЃЌНЋЪ§ОнАДее![]() ЗжГЩ9зщЃЌжЦГЩСЫШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.
ЗжГЩ9зщЃЌжЦГЩСЫШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМ.
ЃЈ1ЃЉЧѓжБЗНЭМЕФ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЩшИУЪага30ЭђОгУёЃЌЙРМЦШЋЪаОгУёжадТОљгУЫЎСПВЛЕЭгк3ЖжЕФШЫЪ§ЃЌЫЕУїРэгЩ.
ЃЈ3ЃЉЙРМЦОгУёдТгУЫЎСПЕФжаЮЛЪ§.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃНјШыИпжаЪ§бЇОКШќИДШќЕФбЇЩњжаЃЌИпвЛФъМЖга8ШЫЃЌИпЖўФъМЖга16ШЫЃЌИпШ§ФъМЖга32ШЫЃЌЯжсгУЗжВуГщбљЕФЗНЗЈДгетаЉбЇЩњжаГщШЁ7ШЫНјаасЗУ.
ЃЈ1ЃЉЧѓгІДгИїФъМЖЗжБ№ГщШЁЕФШЫЪ§ЃЛ
ЃЈ2ЃЉШєДгГщШЁЕФ7ШЫжадйЫцЛњГщШЁ2ШЫзіНјвЛВНСЫНтЃЈзЂИпвЛбЇЩњМЧЮЊ![]() ЃЌИпЖўбЇЩњМЧЮЊ
ЃЌИпЖўбЇЩњМЧЮЊ![]() ЃЌИпШ§бЇЩњМЧЮЊ
ЃЌИпШ§бЇЩњМЧЮЊ![]() ЃЌ
ЃЌ![]()
ЂйСаГіЫљгаПЩФмЕФГщШЁНсЙћЃЛ
ЂкЧѓГщШЁЕФ2ШЫОљЮЊИпШ§ФъМЖбЇЩњЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіПкДќФкзАгаДѓаЁЯрЭЌЕФ5ИіЧђЃЌЦфжа3ИіАзЧђЃЌ2ИіКкЧђЃЌДгжавЛДЮУўГіСНИіЧђЃЎ
ЃЈ1ЃЉЙВгаЖрЩйИіЛљБОЪТМўЃП
ЃЈ2ЃЉУўГіЕФСНИіЖМЪЧАзЧђЕФИХТЪЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСЌајЭЖїЛзгСНДЮЕУЕНЕФЕуЪ§ЗжБ№ЮЊmЃЌnЃЌзїЯђСП![]() ЃЈmЃЌnЃЉЃЌдђ
ЃЈmЃЌnЃЉЃЌдђ![]() гы
гы![]() ЃЈ1ЃЌЉ1ЃЉЕФМаНЧГЩЮЊжБНЧШ§НЧаЮФкНЧЕФИХТЪЪЧ_____ЃЎ
ЃЈ1ЃЌЉ1ЃЉЕФМаНЧГЩЮЊжБНЧШ§НЧаЮФкНЧЕФИХТЪЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁї![]() ЕФШ§ИіФкНЧ
ЕФШ§ИіФкНЧ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЫљЖдгІЕФБпЗжБ№ЮЊ
ЫљЖдгІЕФБпЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌИДЪ§
ЃЌИДЪ§![]() ЃЌ
ЃЌ![]() ЃЌЃЈЦфжа
ЃЌЃЈЦфжа![]() ЪЧащЪ§ЕЅЮЛЃЉЃЌЧв
ЪЧащЪ§ЕЅЮЛЃЉЃЌЧв![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЌВЂЧѓБпГЄ
ЃЌВЂЧѓБпГЄ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉХаЖЯЁї![]() ЕФаЮзДЃЌВЂЧѓЕБ
ЕФаЮзДЃЌВЂЧѓЕБ![]() ЪБЃЌНЧ
ЪБЃЌНЧ![]() ЕФДѓаЁ.
ЕФДѓаЁ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com