
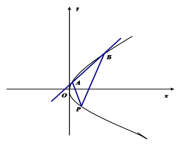
【题目】如图,过抛物线![]() 上一点P(1,-2)作倾斜角互补的两条直线,分别与抛物线交于点
上一点P(1,-2)作倾斜角互补的两条直线,分别与抛物线交于点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 面积的最大值。
面积的最大值。
【答案】(1)y1+y2=4.(2)6
【解析】
(1)因为A(x1,y1),B(x2,y2)在抛物线C:y2=4x上,所以A![]() ,B
,B![]() ,kPA=
,kPA=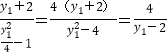 ,同理kPB=
,同理kPB=![]() ,依题意有kPA=-kPB,因为
,依题意有kPA=-kPB,因为![]() =-
=-![]() ,所以y1+y2=4
,所以y1+y2=4
(2)由(1)知kAB=![]() =1,设AB的方程为y-y1=x-
=1,设AB的方程为y-y1=x-![]() ,即x-y+y1-
,即x-y+y1-![]() =0,P到AB的距离为d=
=0,P到AB的距离为d= ,AB=
,AB=![]() ·
·![]() =
=![]() |y1-y2|=2
|y1-y2|=2![]() |2-y1|,所以S△PAB=
|2-y1|,所以S△PAB=![]() ×
× ×2
×2![]() |2-y1|=
|2-y1|=![]() |
|![]() -4y1-12||y1-2|=
-4y1-12||y1-2|=![]() |(y1-2)2-16|·|y1-2|,令y1-2=t,由y1+y2=4,y1≥0,y2≥0,可知-2≤t≤2.S△PAB=
|(y1-2)2-16|·|y1-2|,令y1-2=t,由y1+y2=4,y1≥0,y2≥0,可知-2≤t≤2.S△PAB=![]() |t3-16t|,因为S△PAB=
|t3-16t|,因为S△PAB=![]() |t3-16t|为偶函数,只考虑0≤t≤2的情况,记f(t)=|t3-16t|=16t-t3,f′(t)=16-3t2>0,故f(t)在[0,2]是单调增函数,故f(t)的最大值为f(2)=24,故S△PAB的最大值为6
|t3-16t|为偶函数,只考虑0≤t≤2的情况,记f(t)=|t3-16t|=16t-t3,f′(t)=16-3t2>0,故f(t)在[0,2]是单调增函数,故f(t)的最大值为f(2)=24,故S△PAB的最大值为6


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
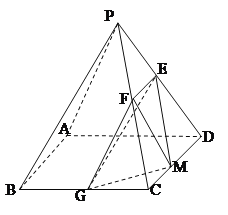
【题目】如图,已知在四棱锥![]() 中,底面
中,底面![]() 是边长为4的正方形,
是边长为4的正方形,![]() 是正三角形,平面
是正三角形,平面![]() 平面
平面![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 是线段
是线段![]() 上一点,求三棱锥
上一点,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某森林公园有一直角梯形区域ABCD,其四条边均为道路,AD∥BC,∠ADC=90°,AB=5千米,BC=8千米,CD=3千米.现甲、乙两管理员同时从![]() 地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.
地出发匀速前往D地,甲的路线是AD,速度为6千米/小时,乙的路线是ABCD,速度为v千米/小时.

(1)若甲、乙两管理员到达D的时间相差不超过15分钟,求乙的速度v的取值范围;
(2)已知对讲机有效通话的最大距离是5千米.若乙先到达D,且乙从A到D的过程中始终能用对讲机与甲保持有效通话,求乙的速度v的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ![]() )的周期为π,且图象上的一个最低点为M(
)的周期为π,且图象上的一个最低点为M(![]() ).
).
(1)求f(x)的解析式及单调递增区间;
(2)当x∈[0,![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
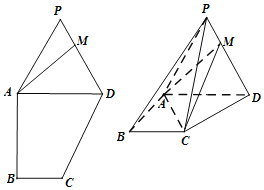
【题目】如图,在多边形PABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,M是线段PD上的一点,且
,M是线段PD上的一点,且![]() ,若将
,若将![]() 沿AD折起,得到几何体
沿AD折起,得到几何体![]() .
.
![]() 证明:
证明:![]() 平面AMC
平面AMC
![]() 若
若![]() ,且平面
,且平面![]() 平面ABCD,求三棱锥
平面ABCD,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把两个全等的正三棱锥的底面粘在一起,在所得的六面体中,所有二面角相等,而顶点可分成两类:在第一类中,每一个顶点发出三条棱;而在第二类顶点中,每一个顶点发出四条棱。试求连结两个第一类顶点的线段长与连结两个第二类顶点的线段长之比。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com