
已知函数f(x)=-x3+ax2-4(a∈R).
(1)若函数y=f(x)的图象在点P(1,f(1))处的切线的倾斜角为 ,求f(x)在[-1,1]上的最小值;
,求f(x)在[-1,1]上的最小值;
(2)若存在x0∈(0,+∞),使f(x0)>0,求a的取值范围.
(1) 最小值为f(0)=-4 (2) (3,+∞)
【解析】(1)f′(x)=-3x2+2ax.
根据题意得,f′(1)=tan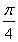 =1,∴-3+2a=1,即a=2.
=1,∴-3+2a=1,即a=2.
∴f(x)=-x3+2x2-4,则f′(x)=-3x2+4x.
令f′(x)=0,得x1=0,x2=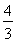 .
.
x | -1 | (-1,0) | 0 | (0,1) | 1 |
f′(x) |
| - | 0 | + |
|
f(x) | -1 | ? | -4 | ? | -3 |
∴当x∈[-1,1]时,f(x)的最小值为f(0)=-4.
(2)∵f′(x)=-3x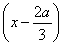 .
.
①若a≤0,则当x>0时,f′(x)<0,∴f(x)在(0,+∞)上单调递减.
又f(0)=-4,则当x>0时,f(x)<-4.
∴当a≤0时,不存在x0>0,使f(x0)>0.
②若a>0,则当0<x< 时,f′(x)>0;
时,f′(x)>0;
当x>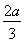 时,f′(x)<0.
时,f′(x)<0.
从而f(x)在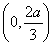 上单调递增,在
上单调递增,在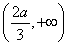 上单调递减.
上单调递减.
∴当x∈(0,+∞)时,f(x)max=f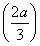 =-
=-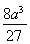 +
+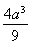 -4=
-4=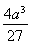 -4.
-4.
根据题意得,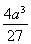 -4>0,即a3>27.∴a>3.
-4>0,即a3>27.∴a>3.
综上可知,a的取值范围是(3,+∞).


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:解答题
设数列{an}的各项都为正数,其前n项和为Sn,已知对任意n∈N*,Sn是a和an的等差中项.
(1)证明数列{an}为等差数列,并求数列{an}的通项公式;
(2)证明 <2.
<2.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
已知 =1-yi,其中x,y是实数,i是虚数单位,则x+yi的共轭复数为( )
=1-yi,其中x,y是实数,i是虚数单位,则x+yi的共轭复数为( )
A.1+2i B.1-2i C.2+i D.2-i
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:解答题
函数f(x)=Asin  +1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为 .
.
(1)求函数f(x)的解析式;
(2)设α∈ ,f
,f  =2,求α的值.
=2,求α的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:选择题
设函数f(x)=sin  +sin
+sin  (ω>0)的最小正周期为π,则( )
(ω>0)的最小正周期为π,则( )
A.f(x)在 上单调递减 B.f(x)在
上单调递减 B.f(x)在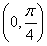 上单调递增
上单调递增
C.f(x)在 上单调递增 D.f(x)在
上单调递增 D.f(x)在 上单调递减
上单调递减
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:填空题
设函数y=f(x),x∈R的导函数为f′(x),且f(x)=f(-x),f′(x)<f(x).则下列三个数:ef(2),f(3),e2f(-1)从小到大依次排列为________.(e为自然对数的底数)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
已知e为自然对数的底数,则函数y=xex的单调递增区间是( )
A.[-1,+∞) B.(-∞,-1]
C.[1,+∞) D.(-∞,1]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第3课时练习卷(解析版) 题型:填空题
关于函数f(x)=lg (x≠0),有下列命题:
(x≠0),有下列命题:
①其图象关于y轴对称;
②当x>0时,f(x)是增函数;当x<0时,f(x)是减函数;
③f(x)的最小值是lg 2;
④f(x)在区间(-1,0)、(2,+∞)上是增函数;
⑤f(x)无最大值,也无最小值.
其中所有正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:填空题
在数列{an}中,a1=1,a2=2,若当整数n>1时,Sn+1+Sn-1=2(Sn+S1)恒成立,则S15=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com