
【题目】在一次高三年级统一考试中,数学试卷有一道满分10分的选做题,学生可以从![]() ,
,![]() 两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.
两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.
(1)若采用随机数表法抽样,并按照以下随机数表,以加粗的数字5为起点,从左向右依次读取数据,每次读取三位随机数,一行读数用完之后接下一行左端.写出样本编号的中位数;
05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74
07 97 10 88 23 09 98 42 99 64 61 71 62 99 15 06 51 29 16 93 58 05 77 09 51
51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48
26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94
14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43
(2)若采用系统抽样法抽样,且样本中最小编号为08,求样本中所有编号之和:
(3)若采用分层轴样,按照学生选择![]() 题目或
题目或![]() 题目,将成绩分为两层,且样本中
题目,将成绩分为两层,且样本中![]() 题目的成绩有8个,平均数为7,方差为4:样本中
题目的成绩有8个,平均数为7,方差为4:样本中![]() 题目的成绩有2个,平均数为8,方差为1.用样本估计900名考生选做题得分的平均数与方差.
题目的成绩有2个,平均数为8,方差为1.用样本估计900名考生选做题得分的平均数与方差.
【答案】(1)![]() ; (2)
; (2)![]() ; (3)平均数为7.2,方差为3.56.
; (3)平均数为7.2,方差为3.56.
【解析】
(1)根据题意读出的编号,将有效编号从小到大排列,由此能求出中位数。
(2)按照系统抽样法,抽出的编号可组成以8为首项,以90为公差的等差数列,由上能求出样本编号之和即。
(3)记样本中8个![]() 题目成绩分别为
题目成绩分别为![]() ,
,![]() ,…
,…![]() ,2个
,2个![]() 题目成绩分别为
题目成绩分别为![]() ,
,![]() ,
,
由题意可知![]() ,
,![]() ,
,![]() ,
,![]() ,由此能用样本估计900名考生选做题得分的平均数,方差。
,由此能用样本估计900名考生选做题得分的平均数,方差。
解:(1)根据题意,读出的编号依次是:
512,916(超界),935(超界),805,770,951(超界),
512(重复),687,858,554,876,647,547,332.
将有效的编号从小到大排列,得
332,512,547,554,647,687,770,805,858,876,
所以中位数为![]() ;
;
(2)由题易知,按照系统抽样法,抽出的编号可组成以8为首项,以90为公差的等差数列,
所以样本编号之和即为该数列的前10项之和,
即![]() ;
;
(3)记样本中8个![]() 题目成绩分别为
题目成绩分别为![]() ,
,![]() ,…
,…![]() ,2个
,2个![]() 题目成绩分别为
题目成绩分别为![]() ,
,![]() ,
,
由题意可知![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
故样本平均数为![]() ;
;
样本方差为![]()
![]()
![]()
![]()
![]() ;
;
所以估计该校900名考生该选做题得分的平均数为7.2,方差为3.56.


科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建造一个矩形游泳池![]() 及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为
及左右两侧两个大小相同的矩形休息区,其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形
,矩形![]() 的一边
的一边![]() 在
在![]() 上,矩形
上,矩形![]() 的一边
的一边![]() 在
在![]() 上,点
上,点![]() 在圆周上,
在圆周上,![]() 在直径上,且
在直径上,且![]() ,设
,设![]() .若每平方米游泳池的造价与休息区造价之比为
.若每平方米游泳池的造价与休息区造价之比为![]() .
.
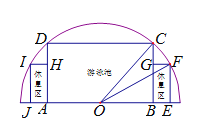
(1)记游泳池及休息区的总造价为![]() ,求
,求![]() 的表达式;
的表达式;
(2)为进行投资预算,当![]() 为何值时,总造价最大?并求出总造价的最大值.
为何值时,总造价最大?并求出总造价的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上一点,且满足
上一点,且满足![]() .
.
(1)求![]() 、
、![]() 的值;
的值;
(2)设![]() 、
、![]() 是抛物线
是抛物线![]() 上不与
上不与![]() 重合的两个动点,记直线
重合的两个动点,记直线![]() 、
、![]() 与
与![]() 的准线的交点分别为
的准线的交点分别为![]() 、
、![]() ,若
,若![]() ,问直线
,问直线![]() 是否过定点?若是,则求出该定点坐标,否则请说明理由.
是否过定点?若是,则求出该定点坐标,否则请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数h(x)是定义在(﹣2,2)上,满足h(﹣x)=﹣h(x),且x∈(0,2)时,h(x)=﹣2x,当x∈(﹣2,0)时,不等式[h(x)+2]2>h(x)m﹣1恒成立,则实数m的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在其图象上存在不同的两点
在其图象上存在不同的两点![]() ,
,![]() ,其坐标满足条件:
,其坐标满足条件:![]() 的最大值为0,则称
的最大值为0,则称![]() 为“柯西函数”,则下列函数:①
为“柯西函数”,则下列函数:①![]() (
(![]() );②
);②![]() (
(![]() );③
);③![]() ;④
;④![]() .其中为“柯西函数”的个数为( )
.其中为“柯西函数”的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() ),其中离心率
),其中离心率![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的动点,
上的动点,![]() 为椭圆的左右焦点,若
为椭圆的左右焦点,若![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 的上顶点,若
的上顶点,若![]() ,试问直线
,试问直线![]() 是否经过定点,若经过定点,求出定点坐标,否则说明理由.
是否经过定点,若经过定点,求出定点坐标,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.
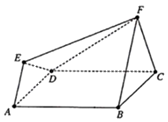
(1)证明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,椭圆
,椭圆![]() 上短轴的一个端点与两个焦点构成的三角形的面积为
上短轴的一个端点与两个焦点构成的三角形的面积为![]() ;
;
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(点
两点(点![]() 在第二象限),
在第二象限),![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点,若
两侧的动点,若![]() ,求证:直线
,求证:直线![]() 的斜率为定值.
的斜率为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com