Question

(21)已知f(x)=(x∈R)在区间［－1,1］上是增函数.

(Ⅰ)求实数a的值所组成的集合A;

(Ⅱ)设关于x的方程f(x)=的两根为x₁、x₂试问:是否存在实数m,使得不等式m²+tm+1≥|x₁－x₂|对任意a∈A及t∈［－1,1］恒成立?若存在,求出m的取值范围;若不存在,请说明理由.

Answer 1

(21)本小题主要考查函数的单调性、导数的应用和不等式等有关知识,考查数形结合及分类讨论思想和灵活运用数学知识分析问题和解决问题的能力.

解：(Ⅰ)f′(x)==,

∵f(x)在［－1,1］上是增函数,

∴f′(x)≥0对x∈［－1,1］恒成立,

即对x∈［－1,1］恒成立.                ①

设(x)=x²－ax－2,

方法一:

∵对x∈［－1,1］,f(x)是连续函数,且只有当a=1时,f′(－1)=0以及当a=－1时,f′(1)=0,

∴A={a|－1≤a≤1}.

方法二:

  0≤a≤1或－1≤a<0

－1≤a≤1.

∵对x∈［－1,1］,f(x)是连续函数,且只有当a=1时,f′(－1)=0以及当a=－1时,f′(1)=0,

∴A={a|－1≤a≤1}.

(Ⅱ)由=,得x²－ax－2=0,

∵Δ=a²+8>0,

∴x₁,x₂是方程x²－ax－2=0的两实根.

∴从而|x₁－x₂|==.

∵－1≤a≤1,∴|x₁－x₂|=≤3.

要使不等式m²+tm+1≥|x₁－x₂|对任意a∈A及t∈［－1,1］恒成立,

当且仅当m²+tm+1≥3对任意t∈［－1,1］恒成立,

即m²+tm－2≥0对任意t∈［－1,1］恒成立.            ②

设g(t)=m²+tm－2=mt+(m²－2),

方法一:

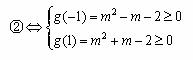
m≥2或m≤－2

所以,存在实数m,使不等式m²+tm+1≥|x₁－x₂|对任意a∈A及t∈［－1,1］恒成立,其取值范围是{m|m≥2或m≤－2}.

方法二:

当m=0时,②显然不成立;

当m≠0时,

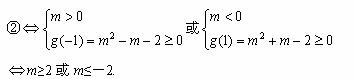
所以,存在实数m,使不等式m²+tm+1≥|x₁－x₂|对任意a∈A及t∈［－1,1］恒成立,其取值范围是{m|m≥2或m≤－2}.