
【题目】如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.
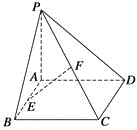
求证:(1)CD⊥PD;(2)EF⊥平面PCD.
【答案】(1)见解析;(2)见解析.
【解析】
试题1)证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高,中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等; (2)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化.
试题解析:(1)∵PA⊥底面ABCD,![]() 平面ABCD
平面ABCD
∴CD⊥PA.
又矩形ABCD中,CD⊥AD,
∵AD∩PA=A,![]() 平面PAD,
平面PAD,![]() 平面PAD
平面PAD
∴CD⊥平面PAD,
![]() 平面PAD∴CD⊥PD.
平面PAD∴CD⊥PD.
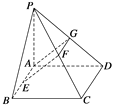
(2)取PD的中点G,连结AG,FG.又∵G、F分别是PD、PC的中点,
∴![]()
∴![]()
∴四边形AEFG是平行四边形,
∴AG∥EF.
∵PA=AD,G是PD的中点,
∴AG⊥PD,∴EF⊥PD,
∵CD⊥平面PAD,AG平面PAD.
∴CD⊥AG.∴EF⊥CD.
∵PD∩CD=D,![]() 平面PCD,CD
平面PCD,CD![]() 平面PCD
平面PCD
∴EF⊥平面PCD.


科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通![]() 座以下私家车投保交强险的基准保费为
座以下私家车投保交强险的基准保费为![]() 元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况想联系,最终保费
元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况想联系,最终保费![]() 基准保费
基准保费![]() (
(![]() 与道路交通事故相联系的浮动比率),具体情况如下表:
与道路交通事故相联系的浮动比率),具体情况如下表:

为了解某一品牌普通![]() 座以下私家车的投保情况,随机抽取了
座以下私家车的投保情况,随机抽取了![]() 辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
类型 |
|
|
|
|
|
|
数量 |
|
|
|
|
|
|
若以这![]() 辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
A. ![]() 元 B.
元 B. ![]() 元 C.
元 C. ![]() 元 D.
元 D. ![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系![]() 自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,求该食品在33℃的保鲜时间.
(2)某药厂生产一种口服液,按药品标准要求其杂质含量不能超过0.01%,若初始时含杂质0.2%,每次过滤可使杂质含量减少三分之一,问至少应过滤几次才能使得这种液体达到要求?(已知![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
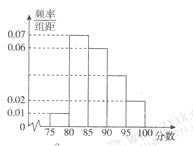
【题目】某高中在今年的期末考试历史成绩中随机抽取![]() 名考生的笔试成绩,作出其频率分布直方图如图所示,已知成绩在
名考生的笔试成绩,作出其频率分布直方图如图所示,已知成绩在![]() 中的学生有1名,若从成绩在
中的学生有1名,若从成绩在![]() 和
和![]() 两组的所有学生中任取2名进行问卷调查,则2名学生的成绩都在
两组的所有学生中任取2名进行问卷调查,则2名学生的成绩都在![]() 中的概率为( )
中的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() 、
、![]() 、
、![]() 、
、![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖,在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
甲说:“![]() 、
、![]() 同时获奖.”
同时获奖.”
乙说:“![]() 、
、![]() 不可能同时获奖.”
不可能同时获奖.”
丙说:“![]() 获奖.”
获奖.”
丁说:“![]() 、
、![]() 至少一件获奖”
至少一件获奖”
如果以上四位同学中有且只有两位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,g(x)=f(x)﹣3.
,g(x)=f(x)﹣3.
(1)判断并证明函数g(x)的奇偶性;
(2)判断并证明函数g(x)在(1,+∞)上的单调性;
(3)若f(m2﹣2m+7)≥f(2m2﹣4m+4)成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com