
(2006
江西,16)已知圆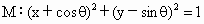 ,直线l∶y=kx,下面四个命题
,直线l∶y=kx,下面四个命题
A
.对任意实数k和θ,直线l和圆M相切B
.对任意实数k和θ,直线l和圆M有公共点C
.对任意实数θ,必存在实数k,使得直线l和圆M相切D
.对任意实数k,必存在实数θ,使得直线l和圆M相切其中真命题的代号是
__________(按照原顺序写出所有真命题的代号).|
答案:B,D 解析:∵圆 M的圆心为(-cosθ,sinθ),满足 . .
∴圆 M是以单位圆 上的任意一点为圆心,半径为1的圆.显然圆M恒过坐标原点. 上的任意一点为圆心,半径为1的圆.显然圆M恒过坐标原点.
直线 l∶y=kx是过坐标原点除y轴以外的所有直线.∴对任意实数 k和θ,直线l和圆M不一定相切,例如,圆心M坐标为(±1,0)时,直线l与圆M不相切.对任意实数 k和θ,直线l和圆M,至少有一个公共点O(坐标原点).当θ=0°时,圆心M坐标为(-1,0),使得直线l和圆M相切的实数k不存在.对任意实数 k,以过坐标原点且垂直于直线l的直线与圆 的交点为圆心的圆必与直线l相切. 的交点为圆心的圆必与直线l相切. |
|
剖析:本题考查直线与圆的位置关系. |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com