
分析 设直线a,b是两条异面直线,其方向向量分别是:$\overrightarrow{m}$和$\overrightarrow{n}$,直线a和b的公垂线的一个方向向量是$\overrightarrow{a}$,则$\left\{\begin{array}{l}\overrightarrow{a}⊥\overrightarrow{m}\\ \overrightarrow{a}⊥\overrightarrow{n}\end{array}\right.$,即$\left\{\begin{array}{l}\overrightarrow{a}•\overrightarrow{m}=0\\ \overrightarrow{a}•\overrightarrow{n}=0\end{array}\right.$,进而可得答案.
解答 解:∵直线a,b是两条异面直线,其方向向量分别是:
$\overrightarrow{m}$=(1,1,1)和$\overrightarrow{n}$=(2,-3,-2),
设直线a和b的公垂线的一个方向向量是$\overrightarrow{a}$=(x,y,z),
则$\left\{\begin{array}{l}\overrightarrow{a}⊥\overrightarrow{m}\\ \overrightarrow{a}⊥\overrightarrow{n}\end{array}\right.$,即$\left\{\begin{array}{l}\overrightarrow{a}•\overrightarrow{m}=0\\ \overrightarrow{a}•\overrightarrow{n}=0\end{array}\right.$,即$\left\{\begin{array}{l}x+y+z=0\\ 2x-3y-2z=0\end{array}\right.$,
令x=1,则$\overrightarrow{a}$=(1,4,-5),
故答案为:(1,4,-5)
答案不唯一(λ,4λ,-5λ),λ≠0均满足条件.
点评 本题考查的知识点是直线的方向向量,向量垂直的充要条件,难度中档.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.
如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
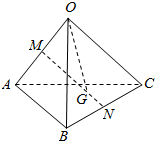 如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.
如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com