
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |
分析 由x>0且x2-xy+2=0,求得y=x+$\frac{2}{x}$,代入x+2y,根据基本不等式性质即可求得x+2y的最小值.
解答 解:x>0且x2-xy+2=0,
则y=x+$\frac{2}{x}$,
∴x+2y=x+2(x+$\frac{2}{x}$)=3x+$\frac{4}{x}$≥2$\sqrt{3x×\frac{4}{x}}$=4$\sqrt{3}$,
当且仅当3x=$\frac{4}{x}$,即x=$\frac{2\sqrt{3}}{3}$,
∴x+2y的最小值4$\sqrt{3}$.
故答案选:A.
点评 本题主要考查基本不等式的应用.基本不等式是在求最值时经常用的方法,是高考的重点内容,要熟练掌握其内容及其变换,属于基础题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{2}$ | C. | -2$\sqrt{2}$ | D. | -2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江苏泰兴中学高二上学期期末数学(文)试卷(解析版) 题型:解答题
已知函数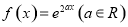 的图像
的图像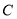 在点
在点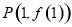 处切线的斜率为
处切线的斜率为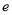 ,记奇函数
,记奇函数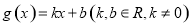 的图像为
的图像为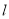 .
.
(1)求实数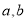 的值;
的值;
(2)当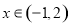 时,图像
时,图像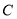 恒在
恒在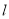 的上方,求实数
的上方,求实数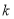 的取值范围;
的取值范围;
(3)若图像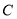 与
与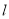 有两个不同的交点
有两个不同的交点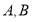 ,其横坐标分别是
,其横坐标分别是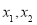 ,设
,设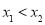 ,求证:
,求证: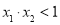 .[来
.[来
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
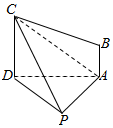 如图,已知平面APD⊥平面ABCD,AB∥CD,CD=AD=AP=4,AB=2,AD⊥AP,CB=2$\sqrt{5}$.
如图,已知平面APD⊥平面ABCD,AB∥CD,CD=AD=AP=4,AB=2,AD⊥AP,CB=2$\sqrt{5}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com