
【题目】如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=BC=2,D,E分别为AA1,B1C的中点.
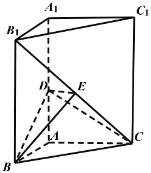
(1)证明:DE⊥平面BCC1B1;
(2)若直线BE与平面AA1B1B所成角为30°,求二面角C﹣BD﹣E的大小.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取BC的中点F,连结AF,EF,推导出DE∥AF,且DE=AF,AF⊥BC,由A1A⊥面ABC,且A1A∥B1B,从而B1B⊥面ABC,进而B1B⊥AF,由此能证明AF⊥平面BCC1B1,从而DE⊥面BCC1B.
(2)过F作FH⊥AB,由题意得FH=1,推导出FH⊥面AA1B1B,即点F到平面AA1B1B的距离为1,EF∥面AA1B1B,E到平面AA1B1B的距离d=1,求出BE=2,EF![]() ,BB1=2
,BB1=2![]() ,以F为原点,FA为x轴,FB为y轴,FE为z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣BD﹣E的大小.
,以F为原点,FA为x轴,FB为y轴,FE为z轴,建立空间直角坐标系,利用向量法能求出二面角C﹣BD﹣E的大小.
(1)证明:取BC的中点F,连结AF,EF,
则EF∥B1B∥DA,且![]() ,
,
∴DE∥AF,且DE=AF,又△ABC是等腰直角三角形,
∴AF⊥BC,由A1A⊥面ABC,且A1A∥B1B,∴B1B⊥面ABC,
∴B1B⊥AF,B1B∩BF=B,∴AF⊥平面BCC1B1,
∴DE⊥面BCC1B.
(2)解:过F作FH⊥AB,由题意得FH=1,
由A1A⊥面ABC,知A1A⊥面ABC,知A1A⊥FH,
∴FH⊥面AA1B1B,即点F到平面AA1B1B的距离为1,
又EF∥B1B,EF平面AA1B1B,∴EF∥面AA1B1B,
∴点E与点F到平面AA1B1B的距离相等,
∴E到平面AA1B1B的距离d=1,
∴sin30°![]() ,解得BE=2,∴EF
,解得BE=2,∴EF![]() ,BB1=2
,BB1=2![]() ,
,
以F为原点,FA为x轴,FB为y轴,FE为z轴,建立空间直角坐标系,
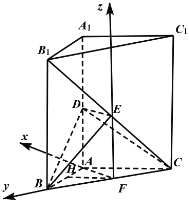
则B(0,![]() ,0),C(0,
,0),C(0,![]() ,0),D(
,0),D(![]() ),E(0,0,
),E(0,0,![]() ),
),
∴![]() (0,2
(0,2![]() ,0),
,0),![]() (
(![]() ),
),![]() (0,
(0,![]() ),
),
设平面CBD和平面BDE的法向量分别为![]() ,
,![]() (x2,y2,z2),
(x2,y2,z2),
则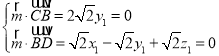 ,取x1=1,得
,取x1=1,得![]() (1,0,﹣1),
(1,0,﹣1),
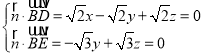 ,取y2=1,得
,取y2=1,得![]() (0,1,1),
(0,1,1),
∴cos![]() ,
,
由图知二面角C﹣BD﹣E是锐二面角,
∴二面角C﹣BD﹣E的大小为![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为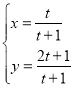 (t为参数),曲线C2的参数方程为
(t为参数),曲线C2的参数方程为![]() (α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(α为参数),以坐标原点为极点.x轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C1的普通方程和曲线C2的极坐标方程;
(Ⅱ)射线![]() 与曲线C2交于O,P两点,射线
与曲线C2交于O,P两点,射线![]() 与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
与曲线C1交于点Q,若△OPQ的面积为1,求|OP|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设α,β是空间中的两个平面,l,m是两条直线,则使得α∥β成立的一个充分条件是( )
A.lα,mβ,l∥mB.l⊥m,l∥α,m⊥β
C.lα,mα,l∥β,m∥βD.l∥m,l⊥α,m⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一、二、三、四年级本科生人数之比为6:5:5:4,则应从一年级中抽取90名学生
B.10件产品中有7件正品,3件次品,从中任取4件,则恰好取到1件次品的概率为![]()
C.已知变量x与y正相关,且由观测数据算得![]() =3,
=3,![]() =3.5,则由该观测数据算得的线性回归方程可能是
=3.5,则由该观测数据算得的线性回归方程可能是![]() =0.4x+2.3
=0.4x+2.3
D.从装有2个红球和2个黑球的口袋内任取2个球,至少有一个黑球与至少有一个红球是两个互斥而不对立的事件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别是双曲线
的左、右顶点分别是双曲线![]() :
:![]() 的左、右焦点,且
的左、右焦点,且![]() 与
与![]() 相交于点(
相交于点(![]() ).
).
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() 与椭圆
与椭圆![]() 交于A,B两点,以线段AB为直径的圆是否恒过定点?若恒过定点,求出该定点;若不恒过定点,请说明理由.
交于A,B两点,以线段AB为直径的圆是否恒过定点?若恒过定点,求出该定点;若不恒过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为
为![]() 上的动点,
上的动点,![]() 为
为![]() 的中点.
的中点.
(1)请求出![]() 点轨迹
点轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() 若直线
若直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() ,弦
,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com