
【题目】已知函数![]() ,
, ![]() .
.
(I)求![]() 的单调区间;
的单调区间;
(II)若对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:对函数求导,针对参数![]() 进行讨论,研究函数得单调性;第二步为恒成立问题,当
进行讨论,研究函数得单调性;第二步为恒成立问题,当![]() 时,由于
时,由于![]() 不满足题意要求,当
不满足题意要求,当![]() 时,求出函数
时,求出函数![]() 的最大值,要使
的最大值,要使![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() ,从而求出
,从而求出![]() 的范围.
的范围.
试题解析:(I)![]() , 当
, 当![]() 时,
时, ![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,令
时,令![]() ,则
,则![]() .则
.则![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
(II)方法1:
当![]() 时,因为
时,因为![]() ,
,
所以不会有![]() ,
, ![]() .
.
②当![]() 时,由(I)知,
时,由(I)知, ![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
所以![]() ,
, ![]() 等价于
等价于![]() .即
.即![]() .
.
设![]() ,由(I)知
,由(I)知![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以
,所以![]() 的解为
的解为![]() .
.
故![]() ,
, ![]() 时,实数
时,实数![]() 的取值范围是
的取值范围是![]() .
.
方法2: ![]() ,
, ![]() 等价于
等价于![]() .令
.令![]() ,则
,则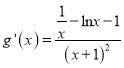 .
.
令![]() ,则
,则![]() .
.
因为当![]() ,
, ![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,可得
,可得![]() 和
和![]() 在
在![]() 上的情况如下:
上的情况如下:
|
|
|
|
| + | 0 | - |
| 单调递增 | 单调递减 |
所以![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
因此![]() ,
, ![]() 等价于
等价于![]() .
.
故![]() ,
, ![]() 时,实数
时,实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】下列三个集合:
①{x|y=x2+1};
②{y|y=x2+1};
③{(x,y)|y=x2+1}.
(1)它们是不是相同的集合?
(2)它们各自的含义是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}
(1)若a=-2,求B∩A,B∩UA;
(2)若BA,求实数a取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .(14分)
.(14分)
(1)此方程表示圆,求m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且![]() (O为坐标原点),求m的值;
(O为坐标原点),求m的值;
(3)在(2)的条件下,求以![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为定义在R上的奇函数,当
为定义在R上的奇函数,当![]() 时,
时,![]() 为二次函数,且满足
为二次函数,且满足![]() ,
,![]() 在
在![]() 上的两个零点为
上的两个零点为![]() 和
和![]() .
.
(1)求函数![]() 在R上的解析式;
在R上的解析式;
(2)作出![]() 的图象,并根据图象讨论关于
的图象,并根据图象讨论关于![]() 的方程
的方程![]()
![]() 根的个数.
根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理:“幂势既同,则积不容异”.它是中国古代一个涉及几何体体积的问题,意思是两个同高的几何体,如在等高处的截面积恒相等,则体积相等.设![]() 为两个同高的几何体,
为两个同高的几何体,![]() 的体积不相等,
的体积不相等,![]() 在等高处的截面积不恒相等,根据祖暅原理可知,
在等高处的截面积不恒相等,根据祖暅原理可知,![]() 是
是![]() 的( )
的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com