
����Ŀ���ҹ��Ŵ���ѧ����������й�ʣ�ඨ�����ֳ������Ӷ�����������������ѧʷ�Ͼ��й�Ե�һҳ��������ѧʷ�����������ijɾͣ�����һֱ������ָ����������ѧ����.�����漰���������������⣬����ѧ˼���ڽ�����ѧ����������ѧ�о����ճ�������Ź㷺Ӧ�ã�Ϊ������ѧ�ķ�չ�����˾��ף���������һ���������⣺��1��2019��2019���������ܱ�5����1�ұ�7����2��������С�����˳���ų�һ�У���������![]() ����ô�����е�����Ϊ�� ��
����ô�����е�����Ϊ�� ��
A.56B.57C.58D.59
 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���![]() �����Σ��ı���
�����Σ��ı���![]() �Ǿ��Σ���ƽ��
�Ǿ��Σ���ƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���е�.
���е�.
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵ�����ֵ.
���������ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������
��ֱ������ϵ![]() ��ֱ��
��ֱ��![]() �IJ���������
�IJ���������![]() ��
��![]() ������.����
Ϊ������.����![]() Ϊ���㣬
Ϊ���㣬 ![]() ��������Ϊ���Ὠ��������ϵ�У�����
��������Ϊ���Ὠ��������ϵ�У�����![]() ��
�� ![]() .
.
��1����![]() ��
�� ![]() ʱ���ж�ֱ��
ʱ���ж�ֱ��![]() ������
������![]() ��λ�ù�ϵ��
��λ�ù�ϵ��
��2����![]() ʱ����ֱ������
ʱ����ֱ������![]() ��
��![]() �ཻ��
�ཻ��![]() ��
�� ![]() ���㣬��
���㣬��![]() ����
����![]() ����ֱ��
����ֱ��![]() ����б��.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�����꼶��ѧ��500�ˣ���������300�ˣ�Ů��200�ˡ�Ϊ���о�ѧ������ѧ�ɼ��Ƿ����Ա��йأ����÷ֲ�����ķ��������г�ȡ��100��ѧ����ͳ�����������п��Ե���ѧ������Ȼ�����Ա��Ϊ�С�Ů���飬�ٽ�����ķ����ֳ�5�飺 ![]() �ֱ����ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
�ֱ����ͳ�ƣ��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��

��I������������С��110�ֵ�ѧ���������ȡ2�ˣ�������ǡΪһ��һŮ�ĸ��ʣ�
��II�����涨������С��130�ֵ�ѧ��Ϊ����ѧ�������������������֪�������2��2�����������ж��Ƿ���90%�İ�����Ϊ����ѧ���������Ա��йء�?
 ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�˶����������Զ��30������������������ֳ�Ԥ���;���������.�±�Ϊ10��ѧ����Ԥ���ɼ�����������������ģ��.
ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
������Զ����λ���ף� | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30������������� | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
����10��ѧ���У�����������Զ��������8�ˣ�ͬʱ����������Զ������30��������������6�ˣ���
��A��2��ѧ������30����������
��B��5��ѧ������30����������
��C��8��ѧ������30����������
��D��9��ѧ������30����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1������![]() ��
��![]() �ϵ����ֵ��
�ϵ����ֵ��
��2��������![]() ������
������![]() ������㣬��
������㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
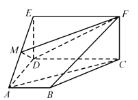
����Ŀ����������ABCD��A1B1C1D1��������A1BC1����ƽ����ȥһ�ǿɵõ���ͼ��ʾ�ļ�����.

��1������BD,BD1,֤��:ƽ��BDD1��ƽ��A1BC1;
��2����֪P,Q,R�ֱ���������ABCDCDD1C1ADD1A1������(���Խ��߽���),֤��:ƽ��PQR��ƽ��A1BC1.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() .
.
��1����![]() ��
��![]() .
.
�ٵ�![]() ʱ��֤����
ʱ��֤����![]() ��
��
����![]() ����������ȵ����
����������ȵ����![]() ����
����![]() ��֤����
��֤����![]() ��
��
��2������![]() �ĵ�����.
�ĵ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��ԲO��x2+y2��4��һ���㣬����A��AB��x�ᣬ����ΪB������D����![]() .
.
��1����D�Ĺ켣C�ķ��̣�
��2����ֱ��x���ֱ��M���켣C��M��N���㣬��P��3��0����ֱ��PM��켣C����һ������ΪQ.�ʣ�ֱ��NQ�Ƿ��һ���㣿�������㣬����ö�������ꣻ���������㣬��˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com