
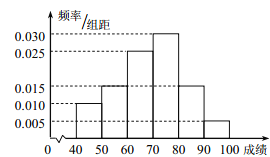
【题目】在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖. 按文理科用分层抽样的方法抽取
)的同学获奖. 按文理科用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图(见下图).
人的成绩作为样本,得到成绩的频率分布直方图(见下图).
(1)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)填写下面的![]() 列联表,能否有超过
列联表,能否有超过![]() 的把握认为“获奖与学生的文理科有关”?
的把握认为“获奖与学生的文理科有关”?
文科生 | 理科生 | 合计 | |
获奖 |
| ||
不获奖 | |||
合计 |
|
附表及公式:
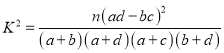 ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)![]() ,
,![]() ;(2)表见解析,有把握.
;(2)表见解析,有把握.
【解析】
试题分析:(1)首先根据频率分布直方图的性质求出![]() 的值,然后根据平均数的定义求解即可;(2)首先根据公式计算出
的值,然后根据平均数的定义求解即可;(2)首先根据公式计算出![]() ,然后与临界表比较,从而作出结论.
,然后与临界表比较,从而作出结论.
试题解析:(1)a=[1-(0.01+0.015+0.03+0.015+0.005)×10]÷10=0.025,
=45×0.1+55×0.15+65×0.25+75×0.3+85×0.15+95×0.05=69. …4分
(2)
文科生 | 理科生 | 合计 | |
获奖 | 5 | 35 | 40 |
不获奖 | 45 | 115 | 160 |
合计 | 50 | 150 | 200 |
…8分
k==≈4.167>3.841,
所以有超过95%的把握认为“获奖与学生的文理科有关”. …12分


科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,图中(1)、(2)、(3)、(4)为她们刺锈最简单的四个图案,这些图案都是由小正方向构成,小正方形数越多刺锈越漂亮,向按同样的规律刺锈(小正方形的摆放规律相同),设第![]() 个图形包含
个图形包含![]() 个小正方形
个小正方形

(1)求![]() 的值
的值
(2)求出![]() 的表达式
的表达式
(3)求证:当![]() 时,
时, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() 为参数), 以坐标原点
为参数), 以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若射线![]() 分别交
分别交![]() 于
于![]() 两点, 求
两点, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,若X是
,若X是![]() 的子集,把X中所有元素的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为
的子集,把X中所有元素的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为![]() 的奇(偶)子集.
的奇(偶)子集.
(1)写出S4的所有奇子集;
(2)求证:![]() 的奇子集与偶子集个数相等;
的奇子集与偶子集个数相等;
(3)求证:当n≥3时,![]() 的所有奇子集的容量之和等于所有偶子集的容量之和.
的所有奇子集的容量之和等于所有偶子集的容量之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就2015年毕业大学生的月收入情况调查了10000人,并根据所得数据画出样本的频率分布直方图所示,每个分组包括左端点,不包括右端点,如第一组表示![]() .
.
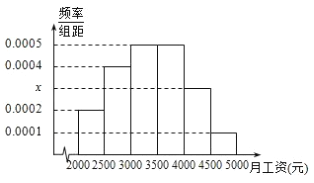
(1)求毕业大学生月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析大学生的收入与所学专业、性别等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com