
| A. | $\frac{1}{4a}$ | B. | $\frac{1}{2a}$ | C. | 2a | D. | 4a |
分析 选择题遵循一般结论利用特殊法,设PQ的斜率 k=0,因抛物线焦点坐标为(0,$\frac{1}{4a}$),把直线方程 y=$\frac{1}{4a}$ 代入抛物线方程得 x=±$\frac{1}{2a}$,可得 PF=FQ=$\frac{1}{2a}$,从而求得结果.
解答 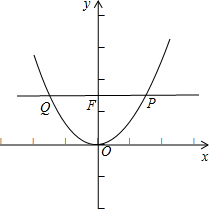 解:不妨设PQ的斜率 k=0,因抛物线焦点坐标为(0,$\frac{1}{4a}$),
解:不妨设PQ的斜率 k=0,因抛物线焦点坐标为(0,$\frac{1}{4a}$),
把直线方程 y=$\frac{1}{4a}$ 代入抛物线方程得 x=±$\frac{1}{2a}$,
∴PF=FQ=$\frac{1}{2a}$,即p=q=$\frac{1}{2a}$,则$\frac{1}{p}+\frac{1}{q}$=2a+2a=4a,
故选:D.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,设k=0,求出PF=FQ=$\frac{1}{2a}$,是解题的关键,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (a-b)2 | B. | (a+b)2 | C. | a2b2 | D. | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
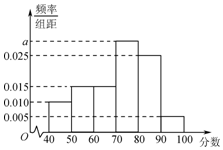 某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),
某校从高一年级学生中随机抽取100名学生,将他们期中考试的数学成绩(均为整数)分成六段:[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示),查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com