
【题目】已知三棱锥A﹣BCD中,AB=CD,且直线AB与CD成60°角,点M、N分别是BC、AD的中点,求直线AB和MN所成的角.
【答案】解:如图,取AC的中点P,连结PM、PN,
则PM∥AB,且PM=![]() AB,PN∥CD,且PN=
AB,PN∥CD,且PN=![]() CD,
CD,
∴∠MPN为AB与CD所成的角(或所成的角的补角),
∴∠MPN=60°或∠MPN=120°,
若∠MPN=60°,∵PM∥AB,∴∠PMN是AB与MN所成的角(或所成角的补角),
又∵AB=CD,∴PM=PN《
∴△PMN是等边三角形,∴∠PMN=60°,
∴AB与MN所成的角为60°;
若∠MPN=120°,则△PMN是等腰三角形,∴∠PMN=30°,
∴AB与MN所成的角为30°,
∴直线AB与MN所成的角为60°或30°.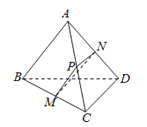
【解析】取AC的中点P,连结PM、PN,则∠MPN为AB与CD所成的角(或所成的角的补角),∠PMN是AB与MN所成的角(或所成角的补角),由此能求出直线AB与MN所成的角.
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识,掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=![]() , 若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
, 若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 过点
过点![]() ,且
,且![]() 和以
和以![]() 为圆
为圆![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)在圆![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出所有的点
,若存在,求出所有的点![]() 的坐标;若不存在说明理由;
的坐标;若不存在说明理由;
(3)若不过![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点,且满足
两点,且满足![]() ,
, ![]() ,
, ![]() 的斜率依次为等比数列,求直线
的斜率依次为等比数列,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 则异面直线BA1与AC1所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数f(x)=ax(a>0,a≠1).
(1)若f(x)的图象过点(1,2),求其解析式;
(2)若 ![]() ,且不等式g(x2+x)>g(3﹣x)成立,求实数x的取值范围.
,且不等式g(x2+x)>g(3﹣x)成立,求实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
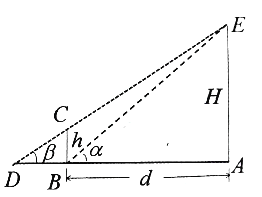
【题目】莫数学建模兴趣小组测量某移动信号塔![]() 的高度
的高度![]() (单位:
(单位: ![]() ),如图所示,垂直放置的标杆
),如图所示,垂直放置的标杆![]() 的高度
的高度![]() ,仰角
,仰角![]() ,
, ![]() .
.
(Ⅰ)该小组已经测得一组![]() 的值,
的值, ![]() ,
, ![]() ,请推测
,请推测![]() 的值;
的值;
(Ⅱ)该小组对测得的多组数据分析后,发现适当调节标杆到信号塔的距离![]() (单位:
(单位: ![]() ),使得
),使得![]() 较大时,可以提高信号塔测量的精确度,若信号塔高度为
较大时,可以提高信号塔测量的精确度,若信号塔高度为![]() ,试问
,试问![]() 为多大时,
为多大时, ![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com