在平面直角坐标系中,点集A={(x,y)|x2+y2≤1},B={(x,y)|x≤4,y≥0,,3x-4y≥0},
则(1)点集P={(x,y)|x=x1+3,y=y1+1,(x1,y1)∈A}所表示的区域的面积为________;
(2)点集Q={(x,y)|x=x1+x2,y=y1+y2,(x1,y1)∈A,(x2,y2)∈B}所表示的区域的面积为________.
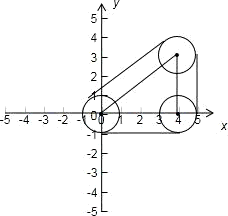
解:(1)由x=x
1+3,y=y
1+1,得x
1=x-3,y
1=y-1,
∵(x
1,y
1)∈A,代入x
2+y
2≤1,
∴(x-3)
2+(y-1)
2≤1,
点集P={(x,y)|x=x
1+3,y=y
1+1,(x
1,y
1)∈A}
所表示的区域是:以(3,1)为圆心、以1为半径的圆,其面积是 π.
(2)由x=x
1+x
2,y=y
1+y
2,得x
1=x-x
2,y
1=y-y
2,
∵(x
1,y
1)∈A,
∴把x
1=x-x
2,y
1=y-y
2,代入x
2+y
2≤1,
∴(x-x
2)
2+(y-y
2)
2≤1
点集Q所表示的区域是以集合B={(x,y)|x≤4,y≥0,,3x-4y≥0},
的区域的边界为圆心轨迹半径为1 的圆内部分,如图
其面积为:5+6+4+3+π=18+π
故答案为:(1) π (2) 18+π
分析:(1)把x=x
1+3,y=y
1+1,中的x
1,y
1代入x
2+y
2≤1,可得点集P的轨迹方程,然后求出点集P所表示的区域的面积.
(2)类似(1)把x=x
1+x
2,y=y
1+y
2,中的x
1,y
1代入x
2+y
2≤1,可得点集Q的轨迹方程,然后求出点Q所表示的区域的面积.
点评:本题考查二元一次不等式组与平面区域的关系问题,考查转化数学思想,作图能力,是难题.

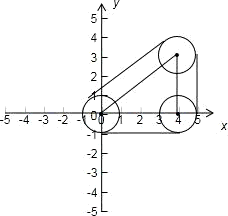 解:(1)由x=x1+3,y=y1+1,得x1=x-3,y1=y-1,
解:(1)由x=x1+3,y=y1+1,得x1=x-3,y1=y-1,

 阅读快车系列答案
阅读快车系列答案