
分析 由A={z||z-1|=1-|z|,z∈C},得A={z||z-1|+|z|=1,z∈C},进一步求出A的轨迹为线段,由B={z||z|<1,z∈C},即可求出B为以(0,0)为圆心的圆,再由z∈A∩(∁UB)=B,即可求出复数z在复平面内对应点的轨迹.
解答 解:由A={z||z-1|=1-|z|,z∈C},得A={z||z-1|+|z|=1,z∈C},即z到M(1,0)和N(0,0)的距离和为1,
∴A为线段MN.
B={z||z|<1,z∈C},即B在以(0,0)为圆心的圆的内部.
∴∁UB表示复平面内以(0,0)为圆心的圆及其外部的点.
若z∈A∩(∁UB),
则复数z在复平面内对应点的轨迹是点N(1,0).
点评 本题考查了复数的代数表示法及其几何意义,考查了复数z在复平面内对应点的轨迹的求法,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | xy-1=0 | B. | xy+1=0 | C. | x-y=0 | D. | x+y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
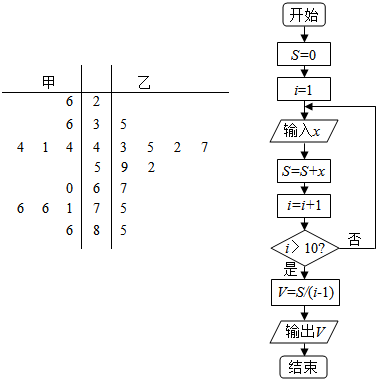 为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.
为了调查网民对甲乙两个网站的关注度,随机抽取了甲乙两个网站9月份某10天在18:00~19:00时段内的点击量(单位:万次),整理后得到如下茎叶图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com