解:(1)由题意,f(x)=x|x|=
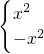
,
任取x
1,x
2∈R,且x
1<x
2当0≤x
1<x
2时,f(x
1)-f(x
2)=x
12-x
22<0;
当x
1<x
2≤0时,f(x
1)-f(x
2)=-x
12+x
22=|x
2|
2-|x
12|<0
当x
1<0<x
2时,f(x
1)-f(x
2)=-x
12-x
22<0
综上所述,f(x)在的上为单调增函数.
(2)在区间(0,+∞)上,函数f(x)=x|x-2m|=|x(x-2m)|,
令g(x)=x(x-2m),它在(0,m)上递减,在上(m,+∞)递增
而在[0,+∞)上,f(x)=
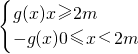
根据二次函数g(x)的性质可知,f(x)在(0,m)上递增,在(m,2m)上递减,在(2m,+∞)上递增
当1∈(0,m]时,即当m≥1时,[f(x)]max=f(1)=2m-1,解得2m-1=m
2,故此时m=1
当1∈(m,2m]时,即
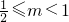
时,此时,[f(x)]max=f(m)=m
2,此时的m均满足题意.
当1∈(2m,+∞)时,即

时,[f(x)]max为f(1)与f(m)中较大者,
而故f(m)=m
2,f(1)=1-2m,故[f(x)]max=m
2当且仅当m
2≥1-2m
解这个不等式,得
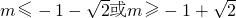
最后将这个范围与

进行交集运算,得m∈[

-1,

)
综上所述,实数m的取值范围是[

-1,1]
(3)容易知道f
1(x)=f(x)=0有且仅有两解2m与0
以下用数学归纳法证明:当n∈N
*时,方程f
n(x)=0有且仅有n+1个解,其中一个解为0,
另n个解均在区间(-∞,2m]中
(i)当n=1时,f
1(x)=0即f(x)=x|x-2m|=0,其有且仅有两个解分别为0和2m,此时命题成立
(ii)假设当n=k,k∈N
*时,命题成立,即方程f
k(x)=0有且仅有k+1个解,其中一个解为0,另k个解均在(-∞,2m]中,将这个k解从小至大依次记为a
1,a
2,a
3,…,a
k当n=k+1时,方程f
k+1(x)=0即f
k(f(x))=0.
该方程成立当且仅当f(x)=a
1,f(x)=a
2,f(x)=a
3,…,f(x)=a
k,f(x)=0之一成立
这k+1个方程的解互不相同,以下研究各个方程解的情况.
f(x)=0的解为2m与0对于方程f(x)=a
i,i=1,2,3,,…,k,是在(-∞,2m]中的常数,
由于a
i<0故方程f(x)=x(x-2m)=a
i的解必定是负数.
当x∈[2m,0)时,由二次函数性质,f(x)=x(x-2m)≥-m
2
由于m∈(-2,0),-m
2>2m≥a
i,于是当x∈[2m,0)时,f(x)>a
1,因此方程f(x)=x|x-2m|=a
i的解必定小于2m
当x∈(-∞,2m)时,方程等f(x)=x|x-2m|=-x
2+2mx,方程f(x)=a
i等价于x
2-2mx+a
i=0,该方程在实数范围内
有两解m±
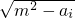
,其中m-
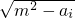
<2m,而m+
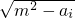
>0>2m
综上所述,当i=1,2,3,,…,k之一时,方程f(x)=a
i有且仅有一个解,且无论i取1,2,3,,…,k中何值,
所得解一定小于2m
这样,算上f(x)=0的两个解0,2m,方程f
k+1(x)=0的解共有k+2个,且其中有一个是0,另k+1个均在(-∞,2m]中,
这表明当n=k+1时,命题同样成立
根据(i)和(ii)可以断定:当n∈N
*时,方程f
n(x)=0有且仅有n+1个解,其中一个解为0,另n个解均在区间(-∞,2m]中,因此所求的解的个数为n+1.
分析:(1)m=0时,f(x)=x|x|=
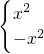
,接下来可以用函数单调性的定义进行证明:设x
1,x
2∈R,且x
1<x
2,分别在x
1,x
2都大于零或都小于零、或其中一个大于零另一个小零情况下得到f(x
1)<f(x
2),所以函数为R上的增函数;
(2)先在(0,+∞)上将原函数变形,变为f(x)=x|x-2m|=|x(x-2m)|,再令g(x)=x(x-2m),通过讨论二次函数g(x)的性质可知,得到它的单调性:f(x)在(0,m)上递增,在(m,2m)上递减,在(2m,+∞)上递增.再讨论自变量1究竟落在哪一个区间内,结合比较f(1)、f(m)的大小,再解相关的不等式,最后综合可得实数m的取值范围是[

-1,1].
(3)当n∈N
*时,方方程f
n(x)=0有且仅有n+1个解,其中一个解为0,另n个解均在区间(-∞,2m]中,因此所求解的个数为n+1.用数学归纳法进行证明:首先验证n=1时,方程f
1(x)=f(x)=0有且仅有两解2m与0,然后再假设当n=k,k∈N
*时,命题成立,通过一元二次方程根的讨论,结合两个实数比较大小,可以证出当n=k+1,k∈N
*时,命题也成立成立,就证出了上述命题.
点评:本题以含有绝对值的函数为例,考查了二次函数的单调性和函数的零点等知识点,属于难题.解题时应该注意分类讨论和转化化归等常用数学思想的运用.

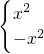 ,
,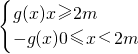
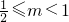 时,此时,[f(x)]max=f(m)=m2,此时的m均满足题意.
时,此时,[f(x)]max=f(m)=m2,此时的m均满足题意. 时,[f(x)]max为f(1)与f(m)中较大者,
时,[f(x)]max为f(1)与f(m)中较大者,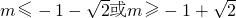
 进行交集运算,得m∈[
进行交集运算,得m∈[ -1,
-1, )
) -1,1]
-1,1]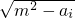 ,其中m-
,其中m-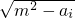 <2m,而m+
<2m,而m+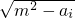 >0>2m
>0>2m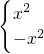 ,接下来可以用函数单调性的定义进行证明:设x1,x2∈R,且x1<x2,分别在x1,x2都大于零或都小于零、或其中一个大于零另一个小零情况下得到f(x1)<f(x2),所以函数为R上的增函数;
,接下来可以用函数单调性的定义进行证明:设x1,x2∈R,且x1<x2,分别在x1,x2都大于零或都小于零、或其中一个大于零另一个小零情况下得到f(x1)<f(x2),所以函数为R上的增函数; -1,1].
-1,1].

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<