
����Ŀ���������ҹ�����������ҵӭ����չ���»�����2016��˫11�ڼ�,ij����ƽ̨������ҵ
���ߴ�1207������������ͬʱ����ع��������Ƴ�����Ե��̵���Ʒ�ͷ����������ϵ���ִ�����ϵͳ��ѡ��200�γɹ����������������۽���ͳ��������Ʒ�ĺ�����Ϊ0.9���Է���ĺ�����Ϊ0.75�����ж���Ʒ�ͷ������������Ľ���Ϊ140��.
(1)������±������ж��Ƿ�����ڷ�������ʲ�����0.5%��ǰ��������Ϊ��Ʒ�������������йأ�
(2)����Ƶ����Ϊ����,ij���ڸù���ƽ̨�Ͻ��е�3�ι�����,�����Ʒ�ͷ���ȫ�����Ĵ���Ϊ�������![]() ��
��
�������Ʒ�ͷ���ȫ�����Ĵ���![]() �ķֲ��У�
�ķֲ��У�
����![]() ����ѧ�����ͷ���.
����ѧ�����ͷ���.

�� ,����
,����![]() ��
��
�Է������ | �Է������� | �ϼ� | |
����Ʒ���� | 140 | ||
����Ʒ������ | 10 | ||
�ϼ� | 200 |
���𰸡�(1) ������(2)������
�������������������1���ȸ���������![]() ������,�����ݴ��뿨����ʽ,�����ղο������жϰ����ʣ�2����ȷ���������ȡ��,�ٸ�����������Ӧ����,�б��ɵ÷ֲ���,��������ѧ������ʽ�Լ����ʽ�������뷽��
������,�����ݴ��뿨����ʽ,�����ղο������жϰ����ʣ�2����ȷ���������ȡ��,�ٸ�����������Ӧ����,�б��ɵ÷ֲ���,��������ѧ������ʽ�Լ����ʽ�������뷽��
����������⣺��1��������ɵù�����Ʒ�ͷ������۵�![]() ��������
��������
�Է������ | �Է������� | �ϼ� | |
����Ʒ���� | 140 | 40 | 180 |
����Ʒ������ | 10 | 10 | 20 |
�ϼ� | 150 | 50 | 200 |
![]()
����![]() �����ڷ�������ʲ�����0.5%��ǰ���£���Ϊ��Ʒ�������������й�.ÿ�ι���ʱ,����Ʒ�ͷ������ĸ���Ϊ
�����ڷ�������ʲ�����0.5%��ǰ���£���Ϊ��Ʒ�������������й�.ÿ�ι���ʱ,����Ʒ�ͷ������ĸ���Ϊ![]() ,
,
��![]() ��ȡֵ������0,1,2,3.
��ȡֵ������0,1,2,3.
����![]() ��
�� ![]() ��
��
![]() ��
�� ![]() .
.
![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 0 | 1 | 2 | 3 |
|
|
|
|
|
����![]() ,��
,��![]() ��
��
![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��x��y����Լ������ 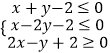 ����z=y��axȡ�����ֵ�����ŽⲻΨһ����ʵ��a��ֵΪ�� ��
����z=y��axȡ�����ֵ�����ŽⲻΨһ����ʵ��a��ֵΪ�� ��
A.![]() ��1
��1
B.2�� ![]()
C.2��1
D.2��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f(x)����x3��ax��
(1)��a=3ʱ,����f(x)�ĵ������䣻
(2)��a=12ʱ������f(x)�ļ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڣ���1��1���ϵĺ���f��x�����㣺f��x����f��y��=f�� ![]() ������x�ʣ���1��0��ʱ����f��x����0����P=f��
������x�ʣ���1��0��ʱ����f��x����0����P=f�� ![]() ��+f��
��+f�� ![]() ����Q=f��
����Q=f�� ![]() ����R=f��0������P��Q��R�Ĵ�С��ϵΪ ��
����R=f��0������P��Q��R�Ĵ�С��ϵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����F1 �� FΪ��ԲC1�� ![]() =1����a1��b1��0����˫����C2�Ĺ������ҽ��㣬�����ڵ�һ�����ڽ��ڵ�M����MF1F2�����߶�MF1Ϊ�ױߵĵ��������Σ���|MF1|=2������ԲC1��������e��[
=1����a1��b1��0����˫����C2�Ĺ������ҽ��㣬�����ڵ�һ�����ڽ��ڵ�M����MF1F2�����߶�MF1Ϊ�ױߵĵ��������Σ���|MF1|=2������ԲC1��������e��[ ![]() ��
�� ![]() ]����˫����C2�������ʵ�ȡֵ��Χ�ǣ� ��
]����˫����C2�������ʵ�ȡֵ��Χ�ǣ� ��
A.[ ![]() ��
�� ![]() ]
]
B.[ ![]() ��++�ޣ�
��++�ޣ�
C.��1��4]
D.[ ![]() ��4]
��4]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���f��x������f��x+1����f��x��=��2x+1��f��2��=15��
��1������f��x���Ľ���ʽ��
��2����g��x��=��2��2m��x��f��x����
��������g��x����x��[0��2]���ǵ�����������ʵ��m��ȡֵ��Χ��
������g��x����x��[0��2]����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��R������f��x��=x|x��a|+2x��
��1����a=2������f��x��������[0��3]�ϵ����ֵ��
��2����a��2��д������f��x���ĵ������䣨����֤������
��3��������a��[��2��4]��ʹ�ù���x�ķ���f��x��=tf��a������������ȵ�ʵ���⣬��ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������x2=2py�ϵ㣨2��2���������߾�����Բ ![]() ���������㣮
���������㣮
��1������ԲE�ķ��̣�
��2������ԲE���϶���A������б��֮��Ϊ��4��ֱ�������Բ����B��C���㣬�Ƿ����һ��D��ʹ��ֱ��BC����õ㣿�����ڣ����������D�����ꣻ�������ڣ���˵�����ɣ�
��3���ڣ�2���������£�����ABC������ΪG������BC�Ķ˵�����ԲE���˶�ʱ����|GA|2+|GB|2+|GC|2��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ ![]() ��ż����,����������⣮
��ż����,����������⣮
��1����ȣ�
��2��������y=f��x����ͼ���������겻�䣬����������Ϊԭ���� ![]() ����������ƽ��
����������ƽ�� ![]() ����λ��Ȼ������ƽ��1����λ�õ�y=g��x����ͼ��������x�ķ���
����λ��Ȼ������ƽ��1����λ�õ�y=g��x����ͼ��������x�ķ��� ![]() ��
�� ![]() ����ֻ��������ͬ�ĸ�����m�ķ�Χ��
����ֻ��������ͬ�ĸ�����m�ķ�Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com