
【题目】设![]() 是实数,函数
是实数,函数![]() .
.
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称点
内恒成立,则称点![]() 为函数
为函数![]() 的“平衡点”.当
的“平衡点”.当![]() 时,试问函数
时,试问函数![]() 是否存在“平衡点”?若存在,请求出“平衡点”的横坐标;若不存在,请说明理由.
是否存在“平衡点”?若存在,请求出“平衡点”的横坐标;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】2019年“中秋节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(![]() )分成七段
)分成七段![]() 后得到如图所示的频率分布直方图,据图解答下列问题:
后得到如图所示的频率分布直方图,据图解答下列问题:
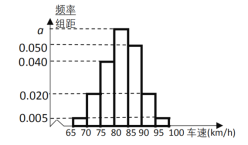
(1)求![]() 的值,并说明交警部门采用的是什么抽样方法?
的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过![]() 即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()

(1)求频率分布直方图中![]() 的值;
的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn,a2+a15=17,S10=55.数列{bn}满足an=log2bn.
(1)求数列{bn}的通项公式;
(2)若数列{an+bn}的前n项和Tn满足Tn=S32+18,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了
两位选手,随机调查了![]() 个学生的评分,得到下面的茎叶图:
个学生的评分,得到下面的茎叶图:
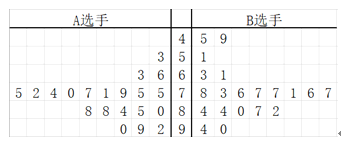
![]() 通过茎叶图比较
通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
![]() 校方将会根据评分记过对参赛选手进行三向分流:
校方将会根据评分记过对参赛选手进行三向分流:
所得分数 | 低于 |
| 不低于 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
记事件![]() “
“![]() 获得的分流等级高于
获得的分流等级高于![]() ”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件
”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,在新高考改革中,打破文理分科的“![]() ”模式初露端倪,其中语、数、外三门课为必考科目,剩下三门为选考科目选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分,假定
”模式初露端倪,其中语、数、外三门课为必考科目,剩下三门为选考科目选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分,假定![]() 省规定:选考科目按考生成绩从高到低排列,按照占总体
省规定:选考科目按考生成绩从高到低排列,按照占总体![]() 、
、![]() 、
、![]() 、
、![]() 分别赋分
分别赋分![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,为了让学生们体验“赋分制”计算成绩的方法,
分,为了让学生们体验“赋分制”计算成绩的方法,![]() 省某高中高一(
省某高中高一(![]() )班(共
)班(共![]() 人)举行了以此摸底考试(选考科目全考,单料全班排名),知这次摸底考试中的物理成绩(满分
人)举行了以此摸底考试(选考科目全考,单料全班排名),知这次摸底考试中的物理成绩(满分![]() 分)频率分布直方图,化学成绩(满分
分)频率分布直方图,化学成绩(满分![]() 分)茎叶图如图所示,小明同学在这次考试中物理
分)茎叶图如图所示,小明同学在这次考试中物理![]() 分,化学
分,化学![]() 多分.
多分.
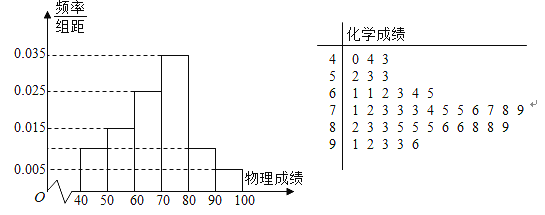
(1)采用赋分制后,求小明物理成绩的最后得分;
(2)若小明的化学成绩最后得分为![]() 分,求小明的原始成绩的可能值;
分,求小明的原始成绩的可能值;
(3)若小明必选物理,其他两科从化学、生物、历史、地理、政治五科中任选,求小明此次考试选考科目包括化学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com