(本小题满分12分)已知函数
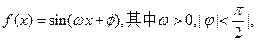
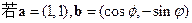
,且
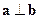
,又知函数

(1)求
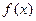
的解析式;
(2)若将
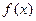
的图象向右平移
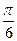
个单位得到
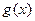
的图象,求
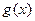
的单调递增区间。
(Ⅰ)
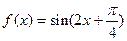
(Ⅱ)
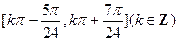
(1)
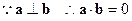
………………1分
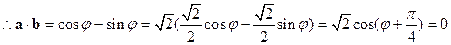
…………3分
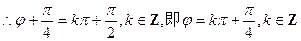
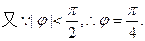
………………5分
∵函数
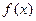
的周期
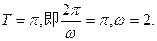
∴解析式为
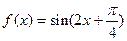
………………6分
(2)由题意知,函数
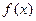
的图象向右平移
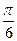
个单位得到
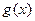
的图象
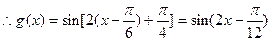
………………8分
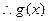
的单调递增区间为
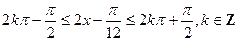
解得
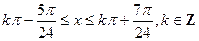
, ………………10分
∴
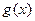
的单调递增区间为
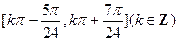
………………12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分) 已知函数
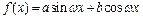
(
 R
R,且
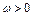
)的部分图象如图所示.
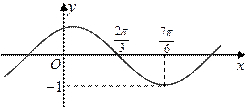
(1) 求
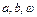
的值;
(2) 若方程
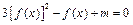
在
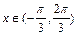
内有两个不同的解,求实数
m的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分13分)
已知函数
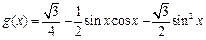
的图象按向量
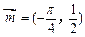
平移得到函数
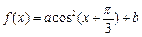
的图象.
(1) 求实数
a、
b的值;
(2) 设函数
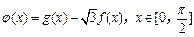
,求函数
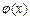
的单调递增区间和最值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
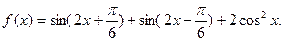
.
(I)求
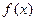
的最小正周期及最大值;
(II)求使
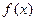
≥2的
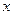
的取值范围
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分10分)
已知向量
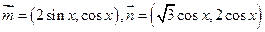
,定义函数
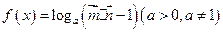
,求函数
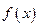
的最小正周期、单调递增区间.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
若
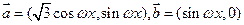
,其中
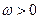
,记函数
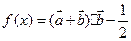
(1)若
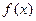
的图像中两条相邻对称轴间的距离
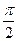
,求
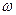
及
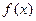
的单调减区间。
(2)在(1)的条件下,且
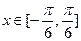
,求最大值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)已知向量
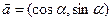
,
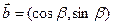
,
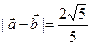
.
(Ⅰ)求
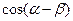
的值;
(Ⅱ)若
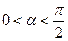
,
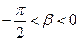
, 且
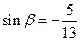
, 求
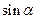
的值。
查看答案和解析>>

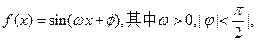
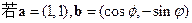 ,且
,且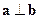 ,又知函数
,又知函数 (1)求
(1)求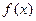 的解析式;
的解析式;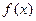 的图象向右平移
的图象向右平移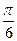 个单位得到
个单位得到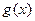 的图象,求
的图象,求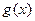 的单调递增区间。
的单调递增区间。 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案