
【题目】在直角坐标系xOy中,已知点P(1,﹣2),直线l: ![]() (m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(1)求直线l和曲线C的普通方程;
(2)求 ![]() +
+ ![]() 的值.
的值.
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判.每局比赛结束时,负的一方在下局当裁判,假设每局比赛中,甲胜乙的概率为 ![]() ,甲胜丙、乙胜丙的概率都是
,甲胜丙、乙胜丙的概率都是 ![]() ,各局比赛的结果相互独立,第一局甲当裁判.
,各局比赛的结果相互独立,第一局甲当裁判.
(1)求第3局甲当裁判的概率;
(2)记前4局中乙当裁判的次数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点F是抛物线τ:x2=2py (p>0)的焦点,点A是抛物线上的定点,且 ![]() =(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1 , k2 .
=(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1 , k2 . 
(I)求抛物线τ的方程;
(Ⅱ)若k1﹣k2=2,点D是点B,C处切线的交点,记△BCD的面积为S,证明S为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为矩形,M是AD上一点.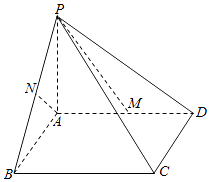
(1)求证:AB⊥PM;
(2)若N是PB的中点,且AN∥平面PCM,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知PC⊥平面ABC,AC=2 ![]() ,PC=BC,AB=4,∠BAC=30°. 点D是线段AB上靠近B的四等分点,PE∥CB,PC∥EB.
,PC=BC,AB=4,∠BAC=30°. 点D是线段AB上靠近B的四等分点,PE∥CB,PC∥EB.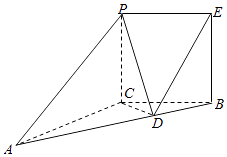
(Ⅰ)证明:直线AB⊥平面PCD;
(Ⅱ)若F为线段AC上靠近C的四等分点,求平面PDF与平面CBD所成锐二面角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第五届北京农业嘉年华于2017年3月11日至5月7日在昌平区兴寿镇草莓博览园中举办,设置“三馆两园一带一谷一线”八大功能板块.现安排六名志愿者去其中的“三馆两园”参加志愿者服务工作,若每个“馆”与“园”都至少安排一人,则不同的安排方法种数为( )
A.C ![]() A
A ![]()
B.5C ![]() A
A ![]()
C.5A ![]()
D.C ![]() A
A ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com