
【题目】设函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,证明:函数
时,证明:函数![]() 不可能存在两个零点.
不可能存在两个零点.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】分析:(Ⅰ)求出函数的导数,![]() 条件下,判断出函数的单调性,求出函数的极值.
条件下,判断出函数的单调性,求出函数的极值.
(Ⅱ)令![]() ,求得两个根,对
,求得两个根,对![]() 分类讨论,分别研究函数的单调性与极值的取值,通过判断即可证明结论.
分类讨论,分别研究函数的单调性与极值的取值,通过判断即可证明结论.
详解:(Ⅰ)解:求导,得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以当![]() 时,
时,![]() ,函数
,函数![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,函数
,函数![]() 为增函数;
为增函数;
故当![]() 时,
时,![]() 存在极小值
存在极小值![]() ,
,![]() 不存在极大值.
不存在极大值.
(Ⅱ)证明:解方程![]() 得
得![]()
当![]() 即
即![]() 时,
时,
随着![]() 的变化,
的变化,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
|
| 1 |
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以函数![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又因为![]() ,
,
所以函数![]() 至多在区间
至多在区间![]() 存在一个零点;
存在一个零点;
当![]() ,即
,即![]() 时,
时,
因为![]() (当且仅当
(当且仅当![]() 时等号成立),
时等号成立),
所以![]() 在
在![]() 单调递减,
单调递减,
所以函数![]() 至多存在一个零点;
至多存在一个零点;
当![]() ,即
,即![]() 时,
时,
随着![]() 的变化,
的变化,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
| 1 |
|
| + | 0 | - | 0 | + |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以函数![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
又因为![]() ,
,
所以当![]() 时,
时,![]() ,
,
综上,当![]() 时,函数
时,函数![]() 不可能存在两个零点.
不可能存在两个零点.


科目:高中数学 来源: 题型:
【题目】《厉害了,我的国》这部电影记录:到2017年底,我国高铁营运里程达2.5万公里,位居世界第一位,超过第二名至第十名的总和,约占世界高铁总量的三分之二.如图是我国2009年至2017年高铁营运里程(单位:万公里)的折线图.

根据这9年的高铁营运里程,甲、乙两位同学分别选择了![]() 与时间变量
与时间变量![]() 的两个回归模型①:
的两个回归模型①:![]() ;②
;②![]() .
.
(1)求![]() ,
,![]() (精确到0.01);
(精确到0.01);
(2)乙求得模型②的回归方程为![]() ,你认为哪个模型的拟合效果更好?并说明理由.
,你认为哪个模型的拟合效果更好?并说明理由.
附:参考公式: ,
,![]() ,
,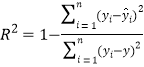 .
.
参考数据:
|
|
|
|
|
|
1.39 | 76.94 | 285 | 0.22 | 0.09 | 3.72 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点, ![]() ,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O=
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O= ![]() .
. 
(1)证明:A′O⊥平面BCDE;
(2)求二面角A′﹣CD﹣B的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个产品有若千零部件构成,加工时需要经过6道工序,分别记为![]() .其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系.若加工工序
.其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系.若加工工序![]() 必须要在工序
必须要在工序![]() 完成后才能开工,则称
完成后才能开工,则称![]() 为
为![]() 的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
工序 |
|
|
|
|
|
|
加工时间 | 3 | 4 | 2 | 2 | 2 | 1 |
紧前工序 | 无 |
| 无 |
|
|
|
现有两台性能相同的生产机器同时加工该产品,则完成该产品的最短加工时间是__________小时.(假定每道工序只能安排在一台机器上,且不能间断).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图所示的程序框图,若输入的k=10,则该算法的功能是( ) 
A.计算数列{2n﹣1}的前10项和
B.计算数列{2n﹣1}的前9项和
C.计算数列{2n﹣1}的前10项和
D.计算数列{2n﹣1}的前9项和
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过曲线的左焦点![]() 且和双曲线实轴垂直的直线与双曲线交于点A,B,若在双曲线的虚轴所在的直线上存在—点C,使得
且和双曲线实轴垂直的直线与双曲线交于点A,B,若在双曲线的虚轴所在的直线上存在—点C,使得![]() ,则双曲线离心率e的最小值为( )
,则双曲线离心率e的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com