
【题目】在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC.BC=2AD=4,EF=3,AE=BE=2,G为BC的中点. 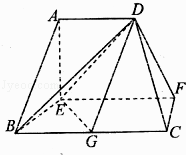
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的正弦值.
【答案】
(1)证明:∵AD∥EF,EF∥BC,∴AD∥BC,
∵BC=2AD,G为BC的中点,∴AD∥BG,且AD=BG,∴四边形ABCD是平行四边形,∴AB∥DG
因为AB不在平面DEG中,DG在平面DEG内,∴AB∥平面DEG
(2)证明:∵EF⊥平面AEB,AE平面AEB,BE平面AEB,
∴EF⊥AE,EF⊥BE,∵AE⊥EB,∴EB、EF、EA两两垂直.
以点E为坐标原点,EB、EF、EA所在直线分别为x、y、z轴建立空间直角坐标系,
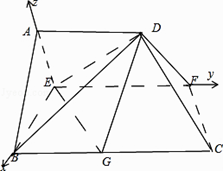
由已知得:A(0,0,2),B(2,0,0),C(2,4,0),D(0,2,2),F(0,3,0),G(2,2,0).
∵ ![]() ,∴
,∴ ![]()
∴BD⊥EG.
(3)解:由已知得 ![]() 是平面EFDA的法向量,设平面DCF的法向量为
是平面EFDA的法向量,设平面DCF的法向量为 ![]()
∵ ![]() ,∴
,∴ ![]() ,令z=1,得x=﹣1,y=2,即
,令z=1,得x=﹣1,y=2,即 ![]() .
.
设二面角C﹣DF﹣E的大小为θ,
则 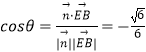 ,∴
,∴ ![]()
∴二面角C﹣DF﹣E的正弦值为 ![]() .
.
【解析】(1)要证AB∥平面DEG,可在平面DEG中找到一条直线与AB平行,根据题目给出的条件,能够证得AB∥DG;(2)根据题目条件先证明EB、EA、EF两两相互垂直,然后以E为原点,以EB、EF、EA所在直线分别为x、y、z轴建立空间直角坐标系,运用向量数量积等于0 ![]() ,从而证明BD⊥EG;(3)在(2)的基础上,求出二面角的两个半平面的法向量,利用法向量求二面角的平面角的余弦值.
,从而证明BD⊥EG;(3)在(2)的基础上,求出二面角的两个半平面的法向量,利用法向量求二面角的平面角的余弦值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱锥A﹣BCD中,△ABC和△BCD所在平面互相垂直,且AB=CD=4,AC=4 ![]() ,CD=4
,CD=4 ![]() ,∠ACB=45°,E,F分别为MN的中点.
,∠ACB=45°,E,F分别为MN的中点. 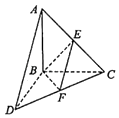
(1)求证:EF∥平面ABD;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足x2﹣4ax+3a2<0,其中a>0,命题q:实数x满足 ![]() . (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
. (Ⅰ)若a=1,且p∧q为真,求实数x的取值范围;
(Ⅱ)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣4=0与直线x﹣2y+1=0交于点p.
(1)求过点p且垂直于直线3x+4y﹣15=0的直线l1的方程;(结果写成直线方程的一般式)
(2)求过点P并且在两坐标轴上截距相等的直线l2方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆经过O(0,0))和A(4,0)两点,线段OA的垂直平分线和圆C交于M,N两点,且|MN|=2 ![]()
(1)求圆C的方程
(2)设点P在圆C上,试问使△POA的面积等于2的点P共有几个?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于实数x的不等式﹣x2+bx+c<0的解集是{x|x<﹣3或x>2},则关于x的不等式cx2﹣bx﹣1>0的解集是( )
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣2,3)
C.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
D.(﹣∞,﹣2)∪(3,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S3=﹣15,且a1+1,a2+1,a4+1成等比数列,公比不为1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.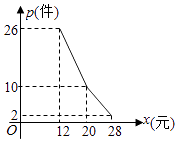
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com