
【题目】学校为了解学生的数学学习情况,在全校高一年级学生中进行了抽样调查,调查结果如表所示:
喜欢数学 | 不喜欢数学 | 合计 | |
男生 | 60 | 20 | 80 |
女生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“男生和女生在喜欢数学方面有差异”;
(2)在被调查的女生中抽出5名,其中2名喜欢数学,现在从这5名学生中随机抽取3人,求至多有1人喜欢数学的概率.
附:参考公式:K2= ![]() ,其中n=a+b+c+d
,其中n=a+b+c+d
P(K2≥k) | 0.100 | 0.050 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
【答案】
(1)解:将2×2列联表中的数据代入公式计算,得
K2= ![]() =
= ![]() =
= ![]() ≈4.762.
≈4.762.
由于4.762>3.841,所以有95%的把握认为“男生和女生在喜欢数学方面有差异”
(2)解:从5名女生中任取3人的一切可能结果所组成的基本事件空间:
Ω={(a1,a2,b1),(a1,a2,b2),(a1,a2,b3),(a1,b1,b2),(a1,b1,b3),
(a1,b2,b3),(a2,b1,b2),(a2,b1,b3),(a2,b2,b3),(b1,b2,b3)},
其中ai表示喜欢数学的学生,i=1,2,bj表示不喜欢数学的学生,j=1,2,3.
Ω由10个基本事件组成,且这些基本事件的出现是等可能的.
用A表示“3人中至多有1人喜欢数学”这一事件,
则A={(a1,b1,b2),(a1,b1,b3),(a1,b2,b3),(a2,b1,b2),
(a2,b1,b3),(a2,b2,b3),(b1,b2,b3)}.
事件A由7个基本事件组成,因而P(A)= ![]()
【解析】(1)将2×2列联表中的数据代入公式计算即可;(2)分别求出所有的基本事件以及满足条件的基本事件,从而求出满足条件的事件的概率即可.


科目:高中数学 来源: 题型:
【题目】若以曲线![]() 上任意一点
上任意一点![]() 为切点作切线
为切点作切线![]() ,曲线上总存在异于
,曲线上总存在异于![]() 的点
的点![]() ,以点
,以点![]() 为切点作切线
为切点作切线![]() ,且
,且![]() ,则称曲线
,则称曲线![]() 具有“可平行性”,现有下列命题:
具有“可平行性”,现有下列命题:
①函数![]() 的图象具有“可平行性”;
的图象具有“可平行性”;
②定义在![]() 的奇函数
的奇函数![]() 的图象都具有“可平行性”;
的图象都具有“可平行性”;
③三次函数![]() 具有“可平行性”,且对应的两切点
具有“可平行性”,且对应的两切点![]() ,
, ![]() 的横坐标满足
的横坐标满足![]() ;
;
④要使得分段函数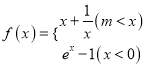 的图象具有“可平行性”,当且仅当
的图象具有“可平行性”,当且仅当![]() .
.
其中的真命题个数有()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B是x轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为x-y+1=0,则直线PB的方程是( ).
A.x+y-5=0
B.2x-y-1=0
C.2y-x-4=0
D.2x+y-7=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断错误的是( )
A.“am2<bm2”是“a<b”的充分不必要条件
B.命题“x∈R,x3﹣x2≤0”的否定是“x∈R,x3﹣x2﹣1>0”
C.“若a=1,则直线x+y=0和直线x﹣ay=0互相垂直”的逆否命题为真命题
D.若p∧q为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 ![]() (t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=
(t为参数),在以直角坐标系的原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ= ![]()
(1)求曲线C的直角坐标方程和直线l的普通方程;
(2)若直线l与曲线C相交于A,B两点,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,点P是CD上的动点,则直线B1P与直线BC1所成的角等于( ) 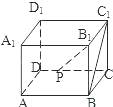
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要制作一个如图的框架(单位:米).要求所围成的总面积为19.5(![]() ),其中
),其中![]() 是一个矩形,
是一个矩形, ![]() 是一个等腰梯形,梯形高
是一个等腰梯形,梯形高![]() ,
, ![]() ,设
,设![]() 米,
米, ![]() 米.
米.
(1)求![]() 关于
关于![]() 的表达式;
的表达式;
(2)如何设计![]() ,
, ![]() 的长度,才能使所用材料最少?
的长度,才能使所用材料最少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在![]() 内的产品为合格品,否则为不合格品,统计结果如表:
内的产品为合格品,否则为不合格品,统计结果如表:
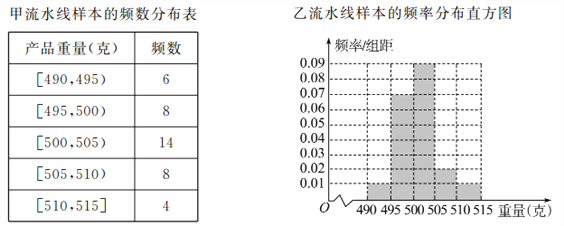
(Ⅰ)求甲流水线样本合格的频率;
(Ⅱ)从乙流水线上重量值落在![]() 内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
内的产品中任取2个产品,求这2件产品中恰好只有一件合格的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com