
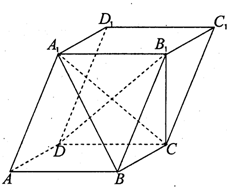
 如题19图,平行六面体ABCD-A1B1C1D1的下底面ABCD是边长为a的正方形,AA1=
如题19图,平行六面体ABCD-A1B1C1D1的下底面ABCD是边长为a的正方形,AA1= a,且点A1在下底面ABCD上的射影恰为D点.
a,且点A1在下底面ABCD上的射影恰为D点. a,AD=a,
a,AD=a, a,∴B1O=
a,∴B1O=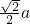 ,∴sin∠B1CA1=
,∴sin∠B1CA1=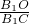 =
= ,∠B1CA1=45°,
,∠B1CA1=45°,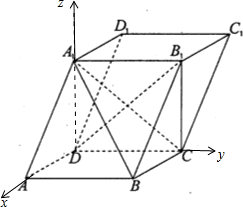
 =(0,a,-a)
=(0,a,-a)  =(-a,0,0)
=(-a,0,0) =(0,0,-a)
=(0,0,-a) =(x,y,z,)则
=(x,y,z,)则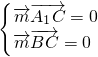 即
即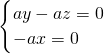
 =(0,1,1)
=(0,1,1) =(x′,y′,z′),则
=(x′,y′,z′),则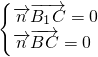 即
即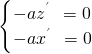 ,
, =(0,1,0)
=(0,1,0)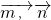 >=
>=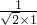 =
= ,<
,<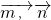 >=45°,又二面角A1-BC-B1的为锐二面角,所以其大小为45°.
>=45°,又二面角A1-BC-B1的为锐二面角,所以其大小为45°. a,AD=a,求出A1D=a,判断出A1B1CD为正方形,再得出 B1D⊥A1C,且BC∩A1C=C,于是B1D⊥面A1CB;
a,AD=a,求出A1D=a,判断出A1B1CD为正方形,再得出 B1D⊥A1C,且BC∩A1C=C,于是B1D⊥面A1CB;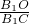 =
= ,求得∠B1CA1=45°;
,求得∠B1CA1=45°; ,平面B1BC的法向量为
,平面B1BC的法向量为  ,利用<
,利用<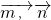 的夹角求出二面角A1-BC-B1的大小.
的夹角求出二面角A1-BC-B1的大小.

科目:高中数学 来源: 题型:
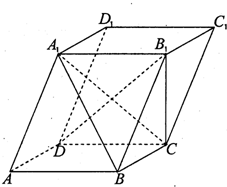 (2011•重庆三模)如题19图,平行六面体ABCD-A1B1C1D1的下底面ABCD是边长为a的正方形,AA1=
(2011•重庆三模)如题19图,平行六面体ABCD-A1B1C1D1的下底面ABCD是边长为a的正方形,AA1=| 2 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三高考前冲刺试卷文数 题型:解答题
(本小题满分12分)
如题19图,平行六面体 的下底面
的下底面 是边长为
是边长为 的正方形,
的正方形, ,且点
,且点 在下底面
在下底面 上的射影恰为
上的射影恰为 点.
点.

(Ⅰ)证明: 面
面 ;
;
(Ⅱ)求二面角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2011年重庆市高考数学三模试卷(理科)(解析版) 题型:解答题
 a,且点A1在下底面ABCD上的射影恰为D点.
a,且点A1在下底面ABCD上的射影恰为D点.
查看答案和解析>>
科目:高中数学 来源:2011年重庆市高考数学三模试卷(文科)(解析版) 题型:解答题
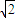 a,且点A1在下底面ABCD上的射影恰为D点.
a,且点A1在下底面ABCD上的射影恰为D点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com