
分析 若关于x的方程${({\frac{3}{2}})^x}=\frac{2+3a}{5-a}$有非负根,则$\frac{2+3a}{5-a}$≥${(\frac{3}{2})}^{0}=1$,解得实数a的取值范围.
解答 解:∵关于x的方程${({\frac{3}{2}})^x}=\frac{2+3a}{5-a}$有非负根,
∴$\frac{2+3a}{5-a}$≥${(\frac{3}{2})}^{0}=1$,
∴$\frac{2+3a}{5-a}-1=\frac{3+4a}{5-a}$≥0,
即$\frac{3+4a}{a-5}≤0$,
解得:$a∈[\frac{3}{4},5)$
点评 本题考查的知识点是根的存在性及根的个数判断,指数的运算性质,二次不等式的解法,难度中档.


科目:高中数学 来源: 题型:解答题
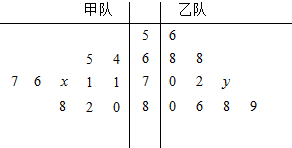 下面的茎叶图记录了甲、乙两代表队各10名同学在一次数学竞赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.
下面的茎叶图记录了甲、乙两代表队各10名同学在一次数学竞赛中的成绩(单位:分),已知甲代表队数据的中位数为76,乙代表队数据的平均数是75.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+y2=4 (-1≤x<$\frac{1}{2}$) | B. | (x-1)2+y2=4 (0≤x<1) | ||
| C. | (x-2)2+y2=4 (-1≤x<$\frac{1}{2}$) | D. | (x-2)2+y2=4 (0≤x<1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{3}$$\sqrt{3}$ | B. | 3 | C. | 8 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | (1,2] | C. | ($\frac{1}{2}$,2] | D. | [$\frac{1}{2}$,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com