
【题目】已知集合A={x|x2﹣6x+5<0},B={x| ![]() <2x﹣4<16},C={x|﹣a<x≤a+3}
<2x﹣4<16},C={x|﹣a<x≤a+3}
(1)求A∪B和(RA)∩B
(2)若A∪C=A,求实数a的取值范围.
【答案】
(1)解:集合A={x|x2﹣6x+5<0}=(1,5),B={x| ![]() <2x﹣4<16}=(2,8),
<2x﹣4<16}=(2,8),
A∪B=(1,8),(RA)∩B=[5,8)
(2)解:若A∪C=A,则CA,
C=,﹣a≥a+3,∴a≤﹣ ![]() .
.
C≠,a>﹣ ![]() ,
, ![]() ,此时﹣
,此时﹣ ![]() <a≤﹣1,
<a≤﹣1,
∴a≤﹣1
【解析】1、本题考查的是不等式集合的交、并、补运算 。
2、本题考查的是不等式集合的交、并、补运算,尤其注意若A∪C=A,则CA,当C=,﹣a≥a+3,∴a≤﹣![]() 的这种情况。
的这种情况。
【考点精析】根据题目的已知条件,利用交、并、补集的混合运算的相关知识可以得到问题的答案,需要掌握求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.


科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() ,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍纵坐标不变)
倍纵坐标不变)
B.向右平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
D.向右平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数y=ax2+x+1(a>0)的图象与x轴两个交点的横坐标分别为x1 , x2 .
(1)证明:(1+x1)(1+x2)=1;
(2)证明:x1<﹣1,x2<﹣1;
(3)若x1 , x2满足不等式|lg ![]() |≤1,试求a的取值范围.
|≤1,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数 ![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A.f(x)是偶函数
B.方程f(f(x))=x的解为x=1
C.f(x)是周期函数
D.方程f(f(x))=f(x)的解为x=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy内,动点P到定点F(﹣1,0)的距离与P到定直线x=﹣4的距离之比为 ![]() .
.
(1)求动点P的轨迹C的方程;
(2)设点A、B是轨迹C上两个动点,直线OA、OB与轨迹C的另一交点分别为A1、B1 , 且直线OA、OB的斜率之积等于- ![]() ,问四边形ABA1B1的面积S是否为定值?请说明理由.
,问四边形ABA1B1的面积S是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a≥0,函数f(x)=(x2﹣2ax)ex , 若f(x)在[﹣1,1]上是单调减函数,则a的取值范围是( )
A.0<a< ![]()
B.![]() <a<
<a< ![]()
C.a≥ ![]()
D.0<a< ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y= ![]() (x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( )
(x>0)图象下方的区域(阴影部分),从D内随机取一个点M,则点M取自E内的概率为( ) 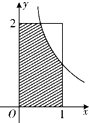
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)满足f(x﹣4)=﹣f(x),且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[﹣8,8]上有四个不同的根x1 , x2 , x3 , x4 , 则x1+x2+x3+x4= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com