
解下列方程或不等式.
(1)3ªA8x=4ªA9x-1;(2)Ax-22+x≥2.
科目:高中数学 来源: 题型:解答题
现有9本不同的书,分别求下列情况的不同分法的种数。
(1)分成三组,一组4本,一组3本,一组2本;
(2)分给三人,一人4本,一人3本,一人2本;
(3)平均分成三组。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将并排的有不同编号的5个房间安排给5个工作人员临时休息,假定每个人可以选择任一房间,且选择各个房间是等可能的,求恰有2个房间无人选择且这2个房间不相邻的安排方式的种数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有多少种(用数字作答).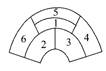
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com