
【题目】如图四棱锥P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2 ![]() ,BC=4
,BC=4 ![]() ,PA=2,点M在线段PD上.
,PA=2,点M在线段PD上.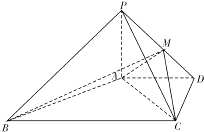
(1)求证:AB⊥PC.
(2)若二面角M﹣AC﹣D的大小为45°,求BM与平面PAC所成的角的正弦值.
【答案】
(1)证明:设E为BC的中点,连接AE,则AD=EC,AD∥EC,
∴四边形AECD为平行四边形,
∴AE⊥BC
∵AE=BE=EC=2 ![]() ,
,
∴∠ABC=∠ACB=45°,
∴AB⊥AC,
∵PA⊥平面ABCD,AB平面ABCD,
∴AB⊥PA
∵AC∩PA=A,
∴AB⊥平面PAC,
∴AB⊥PC
(2)解:设AC∩BD=O,连接OP,过点M作MN⊥AD,过点N作NG⊥AC于G,连接MG,则MN∥PA,
由PA⊥平面ABCD,可得MN⊥平面ABCD,
∴MN⊥AC,
∵NG⊥AC,MN∩NG=N,
∴AC⊥平面MNG,
∴AC⊥MG,
∴∠MGN是二面角M﹣AC﹣D的平面角,即∠MGN=45°
设MN=x,则NG=AG=x,∴AN=ND= ![]() x,
x,
可得M为PD的中点,连接PO交BM于H,连接AH,
由(1)AB⊥平面PAC,∴∠BHA是BM与平面PAC所成的角
在△ABM中,AB=4,AM= ![]() PD=
PD= ![]() ,BM=3
,BM=3 ![]() ,
,
∴cos∠ABM= ![]() ,
,
∵∠BHA与∠ABM互余,
∴BM与平面PAC所成的角的正弦值为 ![]() .
.
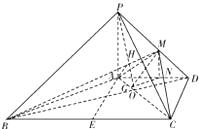
【解析】(1)证明两条异面直线互相垂直,只需证明一条直线垂直于另一条直线所在的平面即可;(2)通过作辅助线在图中表示出所给和要求的二面角,再结合所给条件进行求值即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为迎接2017年“双11”,“双12”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共100个,生产一个汤碗需5分钟,生产一个花瓶需7分钟,生产一个茶杯需4分钟,已知总生产时间不超过10小时.若生产一个汤碗可获利润5元,生产一个花瓶可获利润6元,生产一个茶杯可获利润3元.
(1)使用每天生产的汤碗个数x与花瓶个数y表示每天的利润ω(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语句p:曲线x2﹣2mx+y2﹣4y+2m+7=0表示圆;语句q:曲线 ![]() +
+ ![]() =1表示焦点在x轴上的椭圆,若p∨q为真命题,¬p为真命题,求实数m的取值范围.
=1表示焦点在x轴上的椭圆,若p∨q为真命题,¬p为真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在实数集R中,已知集合A={x| ![]() ≥0}和集合B={x||x﹣1|+|x+1|≥2},则A∩B=( )
≥0}和集合B={x||x﹣1|+|x+1|≥2},则A∩B=( )
A.{﹣2}∪[2,+∞)
B.(﹣∞,﹣2]∪[2,+∞)
C.[2,+∞)
D.{0}∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,圆
,圆![]() .
.
(Ⅰ)若直线![]() 过点
过点![]() 且到圆心
且到圆心![]() 的距离为1,求直线
的距离为1,求直线![]() 的方程;
的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与圆
与圆![]() 交于
交于![]() 两点(
两点(![]() 的斜率为正),当
的斜率为正),当![]() 时,求以线段
时,求以线段![]() 为直径的圆的方程.
为直径的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1=1,an≠0,anan+1=4Sn﹣1.
(Ⅰ)求{an}的通项公式;
(Ⅱ)证明: ![]() +
+ ![]() +…+
+…+ ![]() <2.
<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元.该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(2)设一次订购量为![]() 个,零件的实际出厂单价为
个,零件的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元? (工厂售出一个零件的利润=实际出厂单价-单件成本)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com